All About Rooflines

Part 1 of How To Scale Your Model (Part 0: Introduction | Part 2: TPUs)

하드웨어에서 알고리즘을 실행할 때, 우리는 세 가지 요소에 의해 제한됩니다: 컴퓨터가 수학 연산을 얼마나 빨리 할 수 있는지 (OPs/second), 데이터를 이동시키는 데 사용할 수 있는 대역폭 (bytes/second), 그리고 데이터를 저장하는 데 사용할 수 있는 총 메모리 (bytes)입니다. 이러한 “루프라인(roofline)” 제약 조건은 특정 계산 시간에 대한 상한과 하한을 설정하게 해줍니다.

번역 안내: 원저자(Jacob Austin)의 허락을 받아 원문을 번역 중입니다.
해당 글의 1인칭은 원문 저자를 지칭합니다.
원문: How to Scale Your Model
번역: 신종훈

Where Does the Time Go?

아주 간단한 질문으로 시작해 봅시다: 왜 어떤 알고리즘은 50s나 5ms가 아닌 50ms가 걸릴까요? 모델 내부에서 실제로 상당한 시간이 걸리는 작업은 무엇이며, 얼마나 걸릴 것으로 예상해야 할까요?

계산(Computation): 딥러닝 모델은 사실상 여러 행렬 곱셈 덩어리이며, 각 행렬 곱셈은 부동소수점 곱셈과 덧셈 ‘연산’(FLOPs)으로 구성됩니다. 우리 가속기의 속도가 이 계산에 걸리는 시간을 결정합니다:

\[\begin{equation} T_\text{math} = \frac{\text{Computation FLOPs}}{\text{Accelerator FLOPs/s}} \end{equation}\]

예를 들어, NVIDIA H100은 초당 약 9.89e14 bfloat16bf16은 ML에서 자주 사용되는 16비트 부동소수점 형식인 bfloat16의 줄임말입니다. FLOPs를 수행할 수 있고, TPU v6e는 초당 9.1e14 FLOPs를 수행할 수 있습니다.H100과 B200은 일반적으로 명시된 최대 FLOPs의 약 80-85%만 달성할 수 있는 반면, TPU는 일반적인 사용 환경에서 95%에 더 가까운 성능을 낼 수 있습니다. 이는 H100에서 1e12 FLOPs를 수행하는 데 (대략) 1e12 / 9.89e14 = 1.01ms 가 걸리고, TPU v6e에서는 1e12 / 9.1e14 = 1.1ms 가 걸린다는 의미입니다.이 칩들은 가격이 다르며, 이 결과는 비용을 기준으로 정규화되지 않았음을 유의하세요.

칩 내 통신(Communication within a chip): 가속기 내에서, 텐서는 온칩 메모리(HBM)와 연산 코어(compute cores) 사이에서 이동(transferred)되어야 합니다. 이 연결의 대역폭은 “HBM 대역폭”NVIDIA는 이를 "메모리 대역폭"이라고도 부릅니다. H100에서는, 약 3.35TB/s 이고, TPU v6e에서는 약 1.6TB/s 입니다

칩 간 통신(Communication between chips): 모델을 여러 가속기에 분산시킬 때, 텐서는 번번이 가속기 사이에서 전송되어야 합니다. 우리 하드웨어에는 이를 위한 몇 가지 옵션(ICI, DCN, PCIe)이 있으며, 각각 다른 대역폭을 가집니다.

통신이 칩 내에서 이루어지든 칩 간에 이루어지든, 우리는 이를 bytes/s 단위로 측정하고 총 통신 시간을 다음과 같이 추정합니다:

\[\begin{equation} T_\text{comms} = \frac{\text{Communication Bytes}}{\text{Network/Memory Bandwidth Bytes/s}} \end{equation}\]

일반적으로(항상 그런 것은 아니지만), 단일 칩 내의 계산은 칩 내 및 칩 간 통신과 중첩될 수 있습니다. 이는 계산 시간과 통신 시간 중 최대값을 사용하여 훈련 및 추론 시간의 하한을 알 수 있음을 의미합니다. 또한 그들의 합으로 상한을 알 수 있습니다. 실제로는 최대값을 기준으로 최적화하는데, 대수적으로 더 간단하고 통신과 계산을 중첩시켜 이 한계에 가깝게 도달할 수 있기 때문입니다. 최대값을 염두에 두고 최적화하면 $T_\text{math} + T_\text{comms} \leq 2 * \max(T_\text{math}, T_\text{comms})$ 이므로 하한과 상한은 최대 2배 차이가 납니다. 이후 특정 모델과 대상 시스템을 프로파일링하여 얻을 수 있는 ‘중첩 영역(overlap regions)’과 오버헤드를 모델링하여 이보다 정확도를 높입니다.

\[\begin{equation} T_\text{lower}=\max(T_\text{math}, T_\text{comms}) \end{equation}\] \[\begin{equation} T_\text{upper} = T_\text{math} + T_\text{comms} \end{equation}\]

만약 통신과 계산을 완벽하게 중첩시킬 수 있다고 가정하면, $T_\text{math} > T_\text{comms}$ 일 때 하드웨어가 full utilization이게 됩니다. 이를 “연산 병목(compute-bound)” 상태라고 합니다. $T_\text{comms} > T_\text{math}$ 일 때는 “통신 병목(communication-bound)” 상태가 되는 경향이 있으며, 가속기의 FLOPs/s 중 적어도 일부는 데이터가 오가는 것을 기다리느라 낭비됩니다. 어떤 연산이 연산 병목인지 통신 병목인지를 알 수 있는 한 가지 방법은 “arithmetic intensity” 또는 “operational intensity“를 보는 것입니다.

정의: 알고리즘의 arithmetic intensity는 수행하는 총 FLOPs와 통신해야 하는 바이트 수(칩 내 또는 칩 간)의 비율로 주어집니다.

\[\begin{equation} \text{Arithmetic Intensity} = \frac{\text{Computation FLOPs}}{\text{Communication Bytes}} \end{equation}\]

Arithmetic intensity는 주어진 연산의 “byte 당 FLOPs”를 측정합니다. 대략적으로, Arithmetic intensity가 높을 때 $T_\text{math}$ 은 $T_\text{comms}$ 에 비해 크고, 우리는 일반적으로 사용 가능한 FLOPs의 대부분을 사용합니다. 반대의 경우, 우리는 통신에 더 많은 시간을 소비하고 FLOPs를 낭비합니다. 이 교차가 일어나는 지점이 하드웨어의 “최대 Arithmetic intensity”, 즉 최대 가속기 FLOPs/s와 가속기 대역폭의 비율입니다.

\[\begin{align*} T_\text{math} > T_\text{comms} \Leftrightarrow \frac{\text{Computation FLOPs}} {\text{Accelerator FLOPs/s}} > \frac{\text{Communication Bytes}}{\text{Bandwidth Bytes/s}} & \\[0.5em] \Leftrightarrow \frac{\text{Computation FLOPs}}{\text{Communication Bytes}} > \frac{\text{Accelerator FLOPs/s}}{\text{Bandwidth Bytes/s}} & \\[0.5em] \Leftrightarrow \text{Intensity}(\text{Computation}) > \text{Intensity}(\text{Accelerator}) & \\ \end{align*}\]

$\text{Intensity}(\text{Accelerator})$ 라는 양은 우리 가속기가 최대 FLOPs/s를 달성하는 arithmetic intensity입니다. TPU v5e MXU의 경우, 이는 약 240 FLOPs/byte 입니다MXU는 TPU의 행렬 곱셈 유닛(matrix multiply unit)입니다. 여기서 MXU임을 명시하는 이유는, TPU에는 VPU처럼 원소별 연산을 담당하는 다른 가속기들이 있고, 이들의 최대 FLOPs/s는 다르기 때문입니다., TPU는 1.97e14 FLOPs/s를 수행하고 HBM에서 8.2e11 bytes/s를 로드할 수 있기 때문입니다. 즉, 어떤 알고리즘이 240이는 알고리즘이 HBM에서 가중치를 로드하고 MXU에서 실행되는 경우에만 해당됩니다. 다음 섹션에서 논의하겠지만, 훨씬 더 높은 대역폭을 가진 VMEM에 파라미터를 저장할 수도 있습니다. 많은 알고리즘은 또한 다른 성능 특성을 가진 VPU에서 실행됩니다. FLOPs/byte보다 낮은 arithmetic intensity를 가진다면, 바이트 로딩에 의해 병목이 발생하여 하드웨어를 효율적으로 사용하지 못하게 됩니다.이러한 예시를 하나 살펴보겠습니다:

Example (내적, dot product): bfloat16 정밀도로 두 벡터의 내적, x • y: bf16[N], bf16[N] → bf16[1] 을 계산하려면, 메모리에서 각각 $2 * N = 2N$ bytes인 $x$ 와 $y$ 를 로드하고, $N$ 번의 곱셈과 $N-1$ 번의 덧셈을 수행한 후, $2$ bytes를 HBM에 다시 써야 합니다

\[\begin{equation} \text{Intensity}(\text{dot product}) = \frac{\text{Total FLOPs}}{\text{Total Bytes}} = \frac{N + N - 1}{2N + 2N + 2} = \frac{2N - 1}{4N + 2} \rightarrow \frac{1}{2} \end{equation}\]

$N\rightarrow\infty$ 일 때. 따라서 내적(dot product)의 arithmetic intensity는 $\frac{1}{2}$ 입니다, 다시 말해, 내적은 로드된 바이트당 0.5개의 부동소수점 연산을 수행합니다. 이는 우리의 arithmetic intensity가 하드웨어의 것보다 낮아 통신 병목(communication-bound) 상태가 될 것임을 의미합니다.위의 240이라는 수치는 여기서 올바른 비교는 아닙니다. 다음 섹션에서 보겠지만, 내적(dot-product)은 MXU가 아닌 VPU에서 수행되기 때문입니다. TPU v5p VPU는 약 7e12 FLOPs / second를 수행할 수 있어 critical intensity는 약 3이며, 이는 여기서도 여전히 어느 정도 통신 병목(comms-bound) 상태임을 의미합니다. 어느 쪽이든, intensity가 낮고 일정하다는 사실은 대부분의 하드웨어에서 연산 병목(compute-bound) 상태가 되기 어렵다는 것을 의미합니다.

Visualizing rooflines

메모리와 연산 간의 트레이드오프(tradeoff)를 roofline plot으로 시각화할 수 있습니다. 이는 우리 하드웨어에서 알고리즘의 최대 달성 가능한 FLOPs/s(throughput, y축)를 해당 알고리즘의 arithmetic intensity(x축)에 대해 나타낸 플롯입니다. 다음은 로그-로그(log-log) 플롯의 예입니다:

Figure: 서로 다른 arithmetic intensity를 가진 두 알고리즘(Algo 1과 Algo 2)과 다른 대역폭(BW1, BW2) 하에서의 이론적 최대 처리량을 보여주는 루프라인 플롯 예시입니다. 빨간색 영역에서, 알고리즘은 두 대역폭 모두에서 대역폭 병목 상태이며 하드웨어의 최대 FLOPs/s의 일부를 낭비하고 있습니다. 노란색 영역은 더 낮은 대역폭(BW1)에서만 대역폭 병목 상태입니다. 녹색 영역은 모든 대역폭에서 연산 병목 상태입니다. 여기서는 가속기의 최대 FLOPs/s를 사용하고 있으며, 대역폭을 늘리거나 intensity를 개선해도 이득이 없습니다.

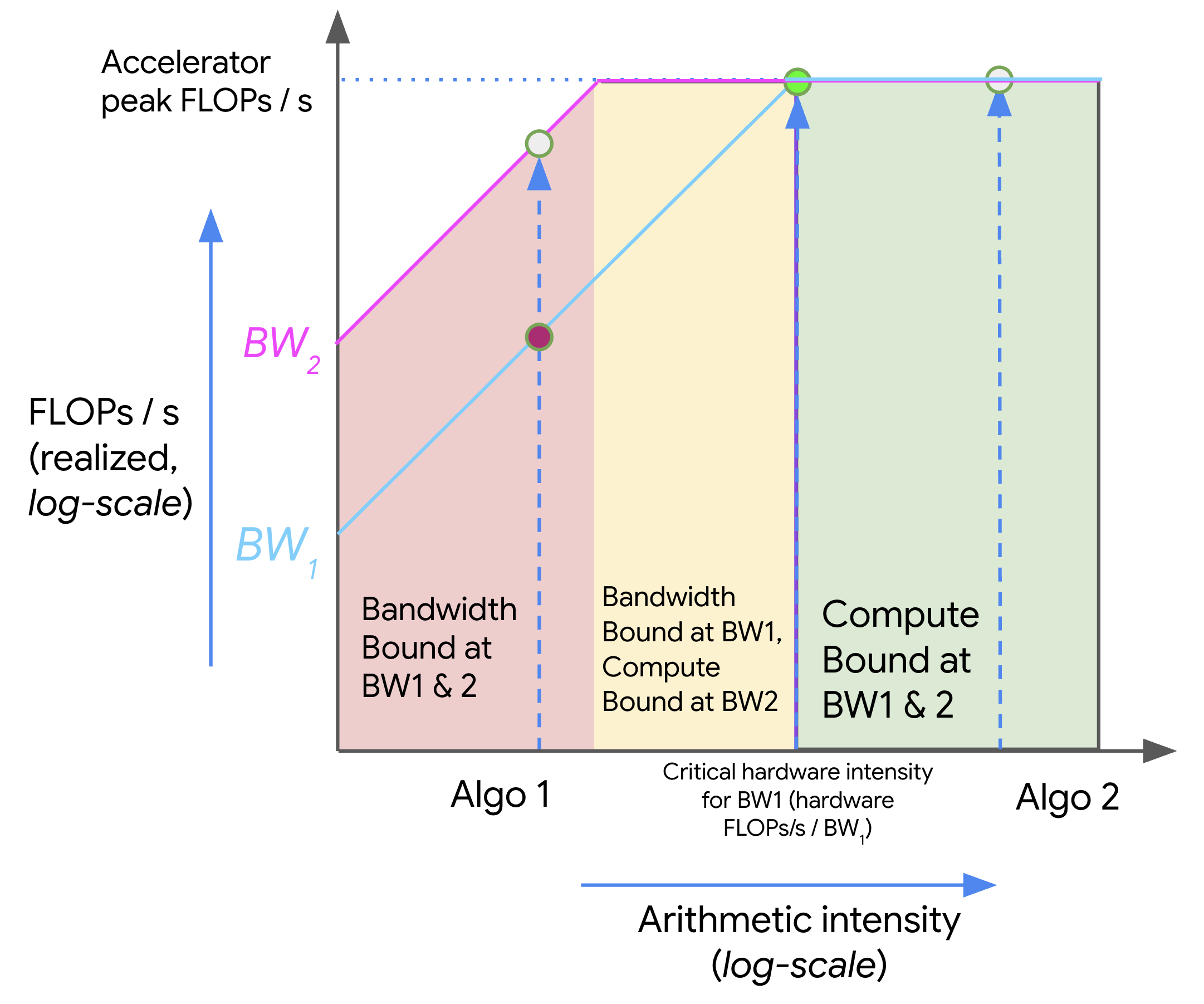
위 플롯에서, intensity가 증가함에 따라(왼쪽에서 오른쪽으로 이동), 알고리즘의 성능(FLOPs/s)은 하드웨어의 critical arithmetic intensity(TPU v5e의 경우 240)에 도달할 때까지 선형적으로 증가합니다. 이보다 낮은 intensity를 가진 알고리즘은 대역폭(BW) 병목 상태가 되며 최대 메모리 대역폭에 의해 제한됩니다(빨간색으로 표시). 오른쪽에 위치한 알고리즘은 우리의 FLOPs를 완전히 활용합니다(녹색으로 표시). 여기서 Algo 1은 통신 병목 상태이며 총 하드웨어 FLOPs/s의 일부만 사용합니다. Algo 2는 연산 병목 상태입니다. 일반적으로 arithmetic intensity를 높이거나 사용 가능한 메모리 대역폭을 늘려(BW1에서 BW2로 이동) 알고리즘의 성능을 향상시킬 수 있습니다.

Matrix multiplication

우리가 곧 가장 좋아하게 될 알고리즘인 행렬 곱셈(일명 matmul)을 살펴보겠습니다. $X * Y \rightarrow Z$ 라고 쓸 때 $X$ 는 $\text{bf16}[B, D]$ 의 shape, $Y$ 는 $\text{bf16}[D, F]$ 의 shape, $Z$ 는 $\text{bf16}[B, F]$ 의 shape입니다. 이 matmul을 수행하려면 $2DF + 2BD$ bytes를 로드하고, $2BDF$ FLOPs를 수행하며, $2BF$ bytes를 다시 써야 합니다.기술적으로는 $BF \times (2D - 1)$ FLOPs를 수행하지만, 이 근사치로도 충분합니다. 이는 $BDF$ 개의 곱셈과 $BF * (D-1)$ 개의 덧셈에서 나옵니다. 섹션 4에서 더 자세히 다룹니다. matmul의 출력은 기술적으로 float32이지만, 보통 HBM으로 다시 복사하기 전에 bfloat16으로 캐스팅합니다. 따라서:

\[\begin{equation} \text{Intensity}(\text{matmul}) = \frac{2BDF}{2BD + 2DF + 2BF} = \frac{BDF}{BD + DF + BF} \end{equation}\]

“배치 크기” $B$가 $D$와 $F$에 비해서 작다고 가정하면 간단한 식으로 만들 수 있습니다. 그러면 다음과 같습니다.

\[\begin{equation} \frac{BDF}{BD + DF + BF} \approxeq \frac{BDF}{DF} = B \end{equation}\] \[\begin{equation} \text{Intensity}(\text{matmul}) > \text{Intensity}(\text{TPU}) \implies B > \frac{1.97e14}{8.20e11} = 240 \end{equation}\]

이는 대부분의 모델에서 로컬 토큰 배치 크기가 $B < 1024$ 이지만 $D$와 $F > 8000$이기 때문에 Transformer matmul에 대해 합리적인 가정입니다. 따라서 로컬 배치 크기가 240 토큰보다 클 때 연산 병목 상태가 된다는 매우 간단한 기준을 얻을 수 있습니다!

Takeaway: bfloat16 matmul이 대부분의 TPU에서 연산 병목 상태가 되려면, 로컬 토큰 배치 크기가 240보다 커야 합니다.이는 일반적인 의미의 배치 크기, 즉 시퀀스 단위의 배치 크기를 의미하는 것이 _아닙니다_. 대부분의 루프라인은 토큰이 동일한 시퀀스에 속하든 다른 시퀀스에 속하든 순전히 토큰 수에만 의존하는 것으로 나타났습니다. 예를 들어, 128개의 GPU에서 4096 토큰으로 구성된 512개 시퀀스의 배치 크기를 사용하는 경우, 총 배치 크기는 '512 * 4096 = 2M' 토큰이고, 로컬 배치 크기는 16k 토큰입니다.

이는 아래 문제들에서 탐구할 몇 가지 주목할 만한 예외 사항을 동반하며, 특히 양자화(quantization)와 관련이 있습니다(예: 활성화를 양자화하지만 여전히 full-precision FLOPs를 수행하는 경우). 하지만 기억해두면 좋은 기준입니다. GPU의 경우 이 숫자는 약간 더 높지만(300에 가깝지만) 대체로 동일한 결론이 적용됩니다. 큰 matmul을 작은 matmul로 분해할 때, 타일 크기도 중요합니다.큰 행렬 곱셈을 수행할 때는 연산을 더 작은 '타일(tile)'로 분해해서, 대역폭이 더 높은 온칩 메모리인 VMEM/SMEM/TMEM에 맞도록 만들어야 합니다. 이 과정에서 데이터 청크(chunk)를 여러 번 로드해야 하므로, 총 로드되는 데이터 양은 더 이상 $O(N^2)$ bytes 라고 단순하게 말할 수 없습니다. 예를 들어, $(m, k) \cdot (k, n)$ matmul의 타일 크기가 $bm$, $bk$, $bm$ 라고 하고 여기서 $tm = m / bm$, 등등 이라고 할 때, 총 FLOPs는 $2 \cdot tm \cdot tn \cdot tk \cdot m \cdot bk \cdot bm$ 이고 총 bytes는 $2 \cdot tm \cdot tn \cdot (tk \cdot (bm \cdot bk + bk \cdot bn) + 2 \cdot bm \cdot bn)$ 입니다. 마지막 항을 무시하면, intensity는 위와 유사하게 $bm \cdot bn / (bm + bn)$ 가 됩니다. lower-level GPU와 TPU의 세부 사항은 다음 섹션에서 논의할 것입니다.

Network communication rooflines

지금까지 논의한 모든 루프라인은 단일 칩 내의 메모리 대역폭 루프라인이었습니다. 이를 기본으로 받아들여서는 안 됩니다. 사실, 이 책에서 우리가 관심을 가질 대부분의 루프라인은 칩 간의 통신을 포함합니다: 보통 여러 TPU에 걸쳐 샤딩된(sharded) 행렬을 포함하는 행렬 곱셈입니다.

다소 작위적인 예를 들어본다면, 2개의 TPU/GPU에 ($D$ 차원을 따라) 균등하게 분할된 두 개의 큰 행렬 $X\sim \text{bfloat16[B, D]}$ 와 $Y \sim \text{bfloat16[D, F]}$ 를 곱하고 싶다고 가정해 봅시다. 이 곱셈을 수행하기 위해 (섹션 3에서 보게 될 것처럼), 각 TPU에서 행렬의 절반을 곱하고 (A = X[:, :D // 2] @ Y[:D // 2, :] 는 TPU 0에서, B = X[:, D // 2:] @ Y[D // 2:, :] 는 TPU 1에서) 그 결과인 “partial sums(부분 합)” 을 다른 TPU로 복사하여 더할 수 있습니다. 각 방향으로 4.5e10 bytes를 복사할 수 있고 각 칩에서 1.97e14 FLOPs/s를 수행할 수 있다고 가정합시다. $T_\text{math}$ 와 $T_\text{comms}$ 는 얼마일까요?

$T_\text{math}$ 는 각 TPU가 작업의 절반을 수행하므로 이전의 절반이 분명합니다, 다시 말하자면두 partial sums을 더하는 데 필요한 FLOPs(또 다른 DF 덧셈)는 무시하고 있습니다만, 이는 거의 무시할 수 있는 수준입니다.

\[T_\text{math} = \frac{2BDF}{2 \cdot \text{Accelerator FLOPs/s}} = \frac{BDF}{1.97e14}\]

그렇다면 $T_\text{comms}$ 는 어떨까요? 이제 이는 칩 간의 통신 시간을 의미합니다! 이는 총 전송된 바이트를 네트워크 대역폭으로 나눈 값입니다, 말하자면

\[T_\text{comms} = \frac{2BF}{\text{Network Bandwidth}} = \frac{2BF}{4.5e10}\]

따라서 우리는 (이제 칩 간 네트워크에 대해) 연산 병목 상태가 될 때는 \(\text{Intensity}(\text{matmul (2-chips)}) > \text{Intensity}(\text{TPU w.r.t. inter-chip network})\) 또는 동등하게 $\frac{BDF}{2BF} = \frac{D}{2} > \frac{1.97e14}{4.5e10} = 4377$ 또는 $D > 8755$ 일 때입니다. 이전과 달리, critical threshhold이 이제 $D$ 에 의존합니다, $B$가 아니라요! 생각해보시면, 이는 단지 하나의 예일 뿐이지만, 이러한 종류의 루프라인이 여러 TPU에 걸쳐 연산을 병렬화할 수 있는 시점을 아는 데 중요하다는 것을 강조할 수 있습니다.

A Few Problems to Work

Question 1 [int8 matmul]: $X[B, D] \cdot_D Y[D, F] \rightarrow Z[B, F]$ 의 행렬 곱셈 연산을 bfloat16 대신 int8 정밀도(파라미터당 1바이트)로 수행한다고 가정해 봅시다.이 문제와 이후에는 $A \cdot_D B$ 표기법을 사용하여 곱셈이 D 차원에 대한 축소를 수행함을 나타낼 것입니다. 이는 아인슈타인 표기법(einsum notation)의 남용입니다.

1. 메모리에서 몇 바이트를 로드해야 하나요? 메모리에 다시 써야 하는 바이트는 몇 개인가요?
2. 총 몇 개의 OPs(연산)가 수행되나요?
3. arithmetic intensity는 얼마인가요?
4. $T_\text{math}$ 과 $T_\text{comms}$ 에 대한 루프라인 추정치는 얼마인가요? 전체 연산의 실행 시간에 대한 현실적인 상한과 하한은 무엇인가요?

HBM 대역폭은 8.1e11 bytes/s 이고 int8의 peak OPs/s는 3.94e14 이라고 가정합니다.(대략 2x bfloat16).

답을 보려면 여기를 클릭하세요.

1. 파라미터를 int8로 저장하므로 파라미터당 1바이트입니다. 따라서 HBM에서 \(BD + DF\) bytes를 로드하고 \(BF\) 를 다시 씁니다.
2. bfloat16과 동일하지만, 이론적으로 int8 OPs/s가 더 빨라야 합니다. 여전히 $2BDF$ FLOPs입니다.
3. Arithmetic intensity 는 \(2BDF / (BD + DF + BF)\)입니다. 위와 동일하게, \(B \ll D\) 이고 \(B \ll F\) 이라고 가정하면, arithmetic intensity는 \(2B\) 가 됩니다. 따라서 우리의 기본 조건은 $B > \text{HBM int8 arithmetic intensity} / 2$ 가 됩니다. 주어진 숫자를 사용하면, 이 int8 intensity는 3.94e14 / 8.1e11 = 486이므로, 최종 조건은 $B > 486 / 2 = 243$ 입니다. 보시면 거의 변하지 않았습니다!
4. \(T_\text{math} = 2BDF / 3.94e14\) 이고 \(T_\text{comms} = (BD + DF + BF) / 8.1e11\) 이여서, 현실적인 하한(lower bound)은 \(\max(T_\text{math}, T_\text{comms})\) 그리고 상한은 \(T_\text{math} + T_\text{comms}\) 입니다.

Question 2 [int8 + bf16 matmul]: In practice we often do different weight vs. activation quantization, 실제로는 가중치와 활성화에 대해 다른 양자화를 사용하는 경우가 많습니다. 가중치는 매우 낮은 정밀도로 저장하고 활성화(및 계산)는 더 높은 정밀도로 유지할 수 있습니다. 가중치는 int8로 양자화하고 활성화(및 계산)는 bfloat16으로 유지하고 싶다고 가정해 봅시다. 어떤 배치 크기에서 연산 병목 상태가 될까요? 1.97e14 bfloat16 FLOPs/s를 가정합니다.

*Hint: $B$ 가 배치 크기일 때 bfloat16[B, D] * int8[D, F] -> bfloat16[B, F] 입니다.

답을 보려면 여기를 클릭하세요.

이전처럼 B가 작다고 가정하면, 2BDF bfloat16 FLOPs를 수행하지만 가중치는 DF 만 필요합니다(bfloat16였다면 2DF). 이는 \(2B > 240\) 또는 \(B > 120\) 일 때 연산 병목(compute-bound) 상태가 됨을 의미합니다. 이는 훨씬 낮은 수치로, 만약 우리가 int8 가중치 양자화(비교적 쉽게 할 수 있음)를 하면서도 bfloat16 FLOPs를 수행할 수 있다면, 효율성 면에서 의미 있는 이득을 얻을 수 있다는 것을 의미합니다(물론 int8 OPs가 더 좋겠지만요).

Question 3: Question 2의 설정을 유지하며, $F = D = 4096$ 와 $F = D = 1024$ 에 대해 peak FLOPs vs. $B$ 의 루프라인 플롯을 만드세요. 근사치가 아닌 정확한 로드된 bytes 수를 사용하세요.

답을 보려면 여기를 클릭하세요.

해당 플롯은 다음과 같습니다:

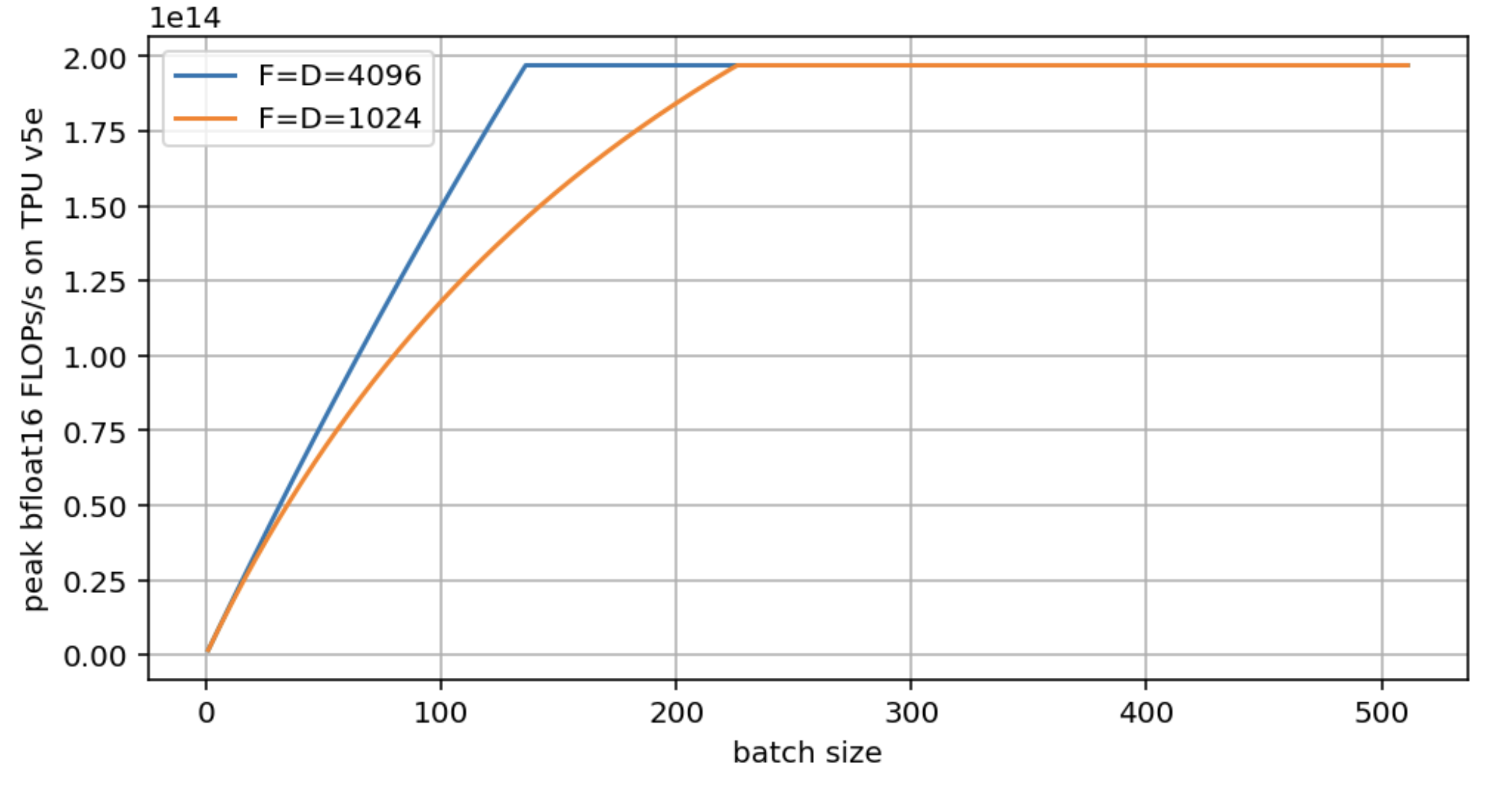
두 모델 모두 결국 최대 하드웨어 FLOPs/s에 도달하지만, 더 큰 D/F가 더 빨리 도달하는 것을 보실 수 있습니다. D=F=1024는 임계(critical) 배치 크기를 거의 두 배로 만듭니다. 위의 플롯을 생성하는 코드는 다음과 같습니다:

import matplotlib.pyplot as plt
import numpy as np

bs = np.arange(1, 512)

def roofline(B, D, F):
  total_flops = 2*B*D*F
  flops_time = total_flops / 1.97e14
  comms_time = (2*B*D + D*F + 2*B*F) / 8.2e11
  total_time = np.maximum(flops_time, comms_time)
  return total_flops / total_time

roofline_big = roofline(bs, 4096, 4096)
roofline_small = roofline(bs, 1024, 1024)

plt.figure(figsize=(8, 4))
plt.plot(bs, roofline_big, label='F=D=4096')
plt.plot(bs, roofline_small, label='F=D=1024')
plt.legend()
plt.xlabel('batch size')
plt.ylabel('peak bfloat16 FLOPs/s on TPU v5e')
plt.grid()

Question 4: 만약 각 배치 element에 대해 다른 행렬이 있다고 가정하며 $\text{int8[B, D]} *_D \text{int8[B, D, F]} \rightarrow \text{int8[B, F]}$ 를 수행한다면, 이 연산의 arithmetic intensity는 얼마인가요?

답을 보려면 여기를 클릭하세요.

총 FLOPs와 통신량을 살펴보는 것으로 시작하겠습니다.

1. 총 FLOPs: FLOPs는 기본적으로 동일합니다. 동일한 수의 \(BD \times DF\) matmuls을 수행하니까요(이는 섹션 4에서 더 자세히 다룹니다). 답은 \(2BDF\) 입니다.
2. 총 통신량: 이 경우에 훨씬 더 많은 통신량이 발생합니다: \(BD + BDF + BF\).
3. 따라서 우리의 arithmetic intensity는 \(2BDF / (BD + BDF + BF)\). 분모에서 \(BDF\) 가 지배적이므로, 대략 \(2\) 입니다. 따라서 배치 크기에 의존하는 대신 본질적으로 상수입니다, 즉 일정하죠. 다만 이는 우리가 거의 항상 통신 병목 상태가 될 것임을 의미하므로 좋은건 아닙니다.

Problem 5 [Memory Rooflines for GPUs]: NVIDIA가 H100에 대해 제공한 스펙 자료를 사용하여, 행렬 곱셈이 연산 병목 상태가 되는 배치 크기를 계산하세요. Tensor Core FLOPs 수치는 실제 값의 두 배의 숫자입니다, 해당 수치는 structured sparsity으로만 달성 가능해서요

답을 보려면 여기를 클릭하세요.

스펙 자료에서 보고된 bfloat16 FLOPs 값은 1.979e15 FLOPs/s이며 “희소성 포함(with sparsity)”이라는 별표가 있습니다. 희소성이 없는 실제 값은 이 값의 절반이므로, 거의 1e15 FLOPs/s에 가깝습니다. 메모리 대역폭은 3.35TB/s, 즉 3.35e12 bytes / second입니다. 따라서 $B_\text{crit}$ 는 1e15 / 3.35e12 = 298 이며, TPU와 상당히 유사합니다.

파트 1은 여기까지입니다! 실제 TPU가 FLOPs와 통신을 어떻게 처리하는지 살펴보는 파트 2를 보려면, 여기를 클릭하세요.