All About Transformer Inference

Part 7 of How To Scale Your Model (Part 6: Training LLaMA | Part 8: Serving LLaMA)

Transformer에서 추론(Inference)을 수행하는 것은 훈련과는 매우 다를 수 있습니다. 부분적으로 이는 추론이 '지연 시간(latency)'이라는 새로운 고려 요소를 추가하기 때문입니다. 이 섹션에서는 모델에서 단일 새 토큰을 샘플링하는 것부터 추론 엔진의 일부로서 많은 가속기 슬라이스에 걸쳐 대규모 Transformer를 효율적으로 확장하는 것까지 모든 과정을 다룰 것입니다.

번역 안내: 원저자(Jacob Austin)의 허락을 받아 원문을 번역 중입니다.
해당 글의 1인칭은 원문 저자를 지칭합니다.
원문: How to Scale Your Model
번역: 신종훈

The Basics of Transformer Inference

Transformer를 훈련시켰고, 이제 이를 사용하여 새로운 시퀀스를 생성하고 싶다고 가정해 봅시다. 결국, 벤치마크 점수가 올라가고 손실 곡선이 내려가는 것은 실제 상황에서 흥미로운 일이 일어날지에 대한 대리 지표일 뿐입니다!역사적으로, 추론 코드를 전혀 건드리지 않고도 놀라울 정도로 많은 Transformer 연구를 수행할 수 있었습니다 — LLM 손실, 객관식 벤치마크는 적절한 KV 캐시나 생성 루프 구현 없이도 효율적으로 실행될 수 있습니다. 이는 특히 연구 코드베이스에서 추론 코드 경로에 손쉽게 얻을 수 있는 성과(low hanging fruits)가 많다는 것을 의미합니다.

샘플링은 개념적으로 간단합니다. 시퀀스를 입력하면 우리의 Transformer가 \(\log p(\text{next token}_i \vert \text{previous tokens})\), 즉 가능한 모든 다음 토큰에 대한 로그 확률을 뱉어낼 것입니다. 이 분포에서 샘플링하여 새로운 토큰을 얻을 수 있습니다. 이 토큰을 추가하고 이 과정을 반복하면 프롬프트의 연속인 토큰 시퀀스를 얻게 됩니다.

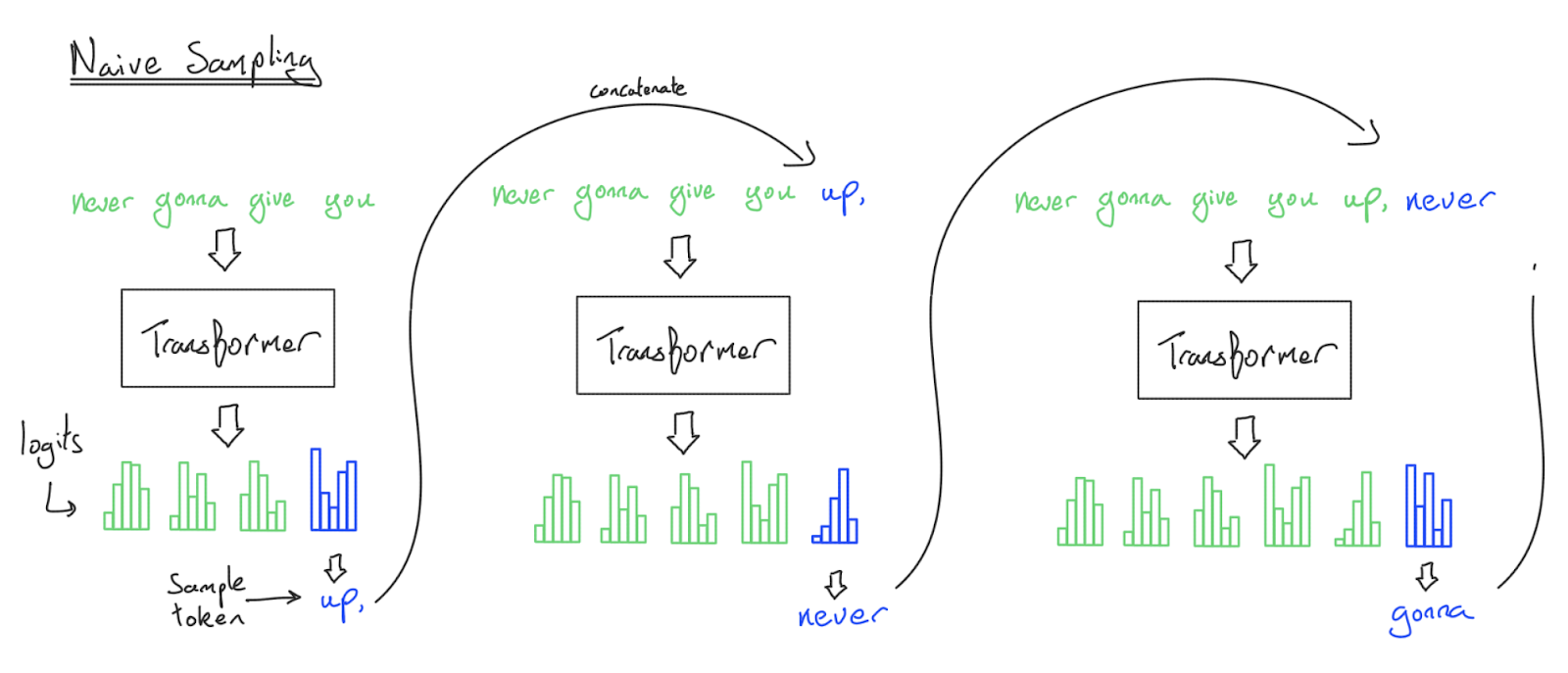
Figure: Transformer로부터의 순진한(naive) 샘플링. 파란색 로짓(logits)은 샘플링할 수 있는 다음 토큰에 대한 분포를 제공합니다. 각 단계가 전체 접두사를 다시 처리하여 알고리즘의 $\Theta(n^2)$ 실행 시간을 초래한다는 점에 유의하세요.

방금 Transformer 샘플링의 순진한 구현을 설명했지만, 작동은 하더라도 실제로는 절대 이렇게 하지 않습니다. 토큰을 생성할 때마다 전체 시퀀스를 다시 처리하기 때문입니다. 이 알고리즘은 \(n\)개의 토큰을 생성하기 위해 FFW에서 \(O(n^2)\), 어텐션 메커니즘에서 \(O(n^3)\)의 복잡도를 가집니다!

어떻게 이를 피할 수 있을까요? 매번 전체 순방향 패스를 수행하는 대신, 각 순방향 패스에서 이전 토큰을 다시 처리하지 않도록 하는 중간 활성화를 저장할 수 있습니다. 구체적으로, 주어진 토큰은 내적 어텐션(dot-product attention) 동안 이전 토큰에만 주의를 기울이기 때문에, 각 토큰의 키(key)와 값(value) 프로젝션을 KV cache라는 새로운 데이터 구조에 쓰기만 하면 됩니다. 과거 토큰에 대한 키/값 프로젝션을 저장하고 나면, 미래의 토큰은 이전 토큰에 대해 새로운 FLOPs를 수행하지 않고 단순히 \(q_i \cdot k_j\) 내적을 계산할 수 있습니다. 놀랍죠!

이를 염두에 두고, 추론에는 두 가지 핵심 부분이 있습니다:

다음은 KV 캐시를 사용한 샘플링 다이어그램입니다:

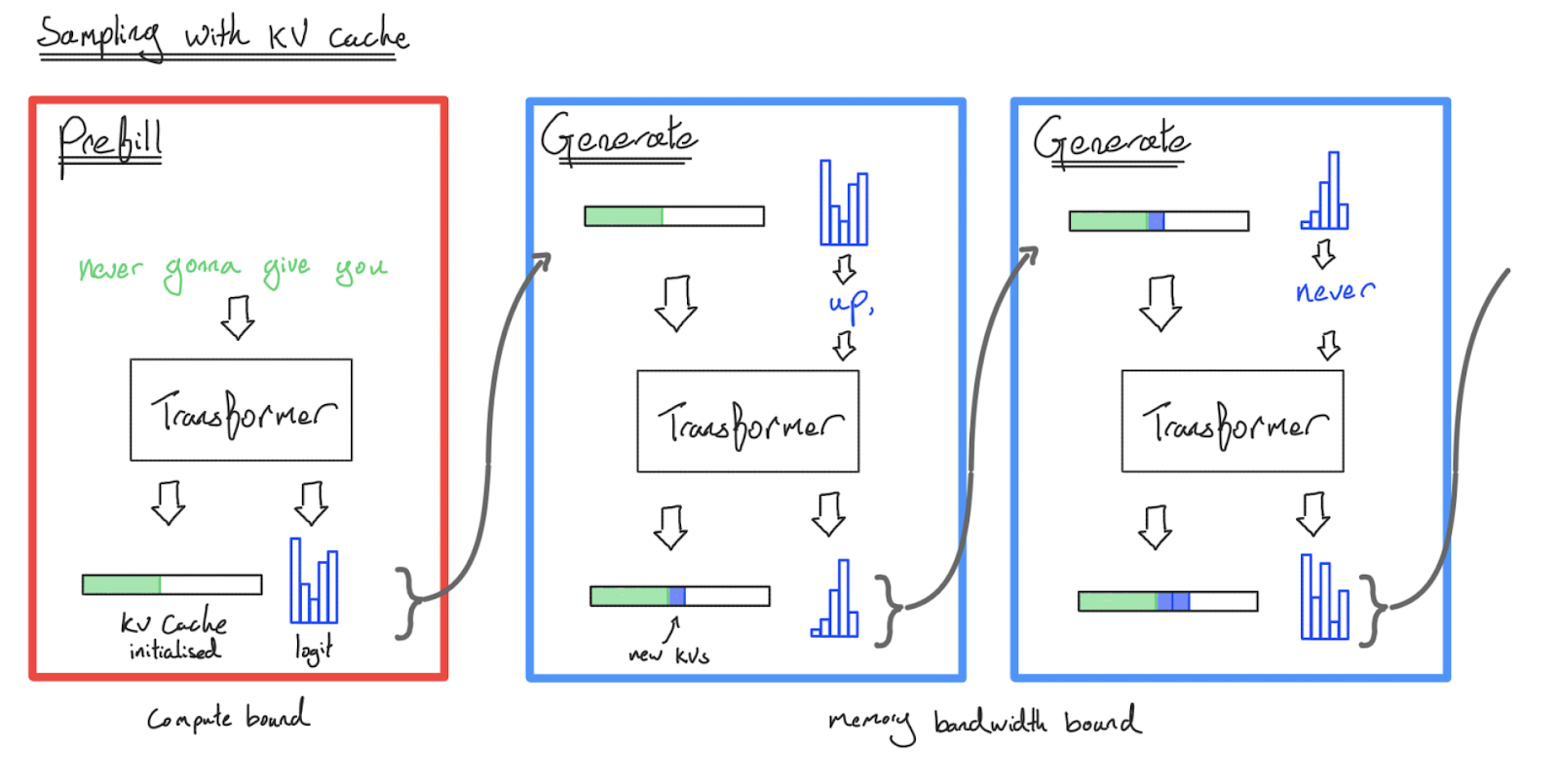
Figure: KV 캐시를 사용한 효율적인 Transformer 샘플링 다이어그램. Prefill은 프롬프트를 처리하고 모든 토큰별 키-값 활성화를 캐시에 저장합니다. Generation은 이 캐시(및 마지막 토큰 로짓)를 가져와 새 토큰을 샘플링하고, 새 토큰을 모델에 통과시켜 KV 캐시에 주의를 기울이고 새 토큰의 키-값 프로젝션을 캐시에 다시 저장합니다. 이는 MLP 블록에서 $O(n)$ 알고리즘입니다.

KV 캐시로 샘플링함으로써, 이전 토큰을 다시 처리하지 않기 때문에 $n$개의 토큰을 생성하는 시간 복잡도를 FFW에서 \(O(n)\), 어텐션에서 \(O(n^2)\)로 줄였습니다. 그러나 시퀀스를 생성하려면 여전히 많은 순방향 패스가 필요합니다 — Gemini나 ChatGPT에 쿼리하고 결과가 스트리밍되어 돌아올 때 일어나는 일이 바로 이것입니다. 모든 토큰은 거대한 모델에 대한 (일반적으로) 별도의 (하지만 부분적으로 캐시된) Transformer 호출입니다.

곧 prefill과 generation이 매우 다른 야수라는 것을 보게 될 것입니다 —— Transformer 추론은 변장한 두 가지 작업입니다! 훈련과 비교할 때, KV 캐시는 또한 새롭고 중요한 복잡성의 원천입니다.

What do we actually want to optimize?

더 진행하기 전에, 추론의 완전히 새로운 측면인 지연 시간(latency)을 강조할 가치가 있습니다. 훈련 중에는 처리량(칩당 초당 처리된 총 토큰 수)에만 관심을 갖는 반면, 추론 중에는 토큰을 얼마나 빨리 생성하는지(Time To First Token (TTFT) 및 토큰당 지연 시간)에 대해 걱정해야 합니다. 예를 들어:

하드웨어 활용률을 극대화하는 것은 여전히 중요하며 비용과 TTFT에 도움이 되지만, 훈련과 달리 모든 상황에서 개별 사용자에게 더 나은 경험으로 반드시 이어지는 것은 아닙니다. 가속기, 시스템 및 모델 아키텍처 수준에서의 많은 최적화는 지연 시간, 처리량, 컨텍스트 길이, 심지어 모델 품질 간의 트레이드오프를 만듭니다.

A more granular view of the Transformer

지금까지 우리는 Transformer를 주로 피드포워드 블록의 스택으로 취급했습니다. 이는 FLOPs와 메모리 관점에서는 합리적인 경우가 많지만, 추론을 적절히 모델링하기에는 충분하지 않습니다.이 섹션 전체에서 알 수 있는 한 가지 사실은 추론이 훈련보다 훨씬 덜 관대하다는 것입니다. 우리는 일반적으로 훨씬 적은 FLOPs, 배치 기회가 적고, 지연 시간에 훨씬 더 민감합니다. KV 캐시 또한 추론을 극적으로 복잡하게 만듭니다. Part 4에서 보았듯이 Transformer 순방향 패스의 주요 구성 요소는 다음과 같습니다:

  1. 다수의 선형 연산, MLP ($W_{in}$, $W_{out}$) 및 어텐션 QKV 프로젝션과 출력 프로젝션 ($W_Q$, $W_K$, $W_V$, $W_O$)을 포함합니다. 이들은 모두 HBM에서 파라미터와 활성화 배치를 읽고, FLOPs를 수행하고, 결과를 HBM에 다시 쓰는 것을 포함합니다.
  2. 내적 어텐션(Dot-product attention). HBM에서 키-값 프로젝션 배치와 쿼리 활성화 배치를 읽고, 몇 번의 내적과 softmax 연산을 수행하고, 어텐션 결과를 HBM에 다시 써야 합니다.
  3. 그 외 모든 것, layer norm 적용, 활성화 함수, 토큰 샘플링, KV 캐시 업데이트, 위치 임베딩 등을 포함합니다. 이들은 약간의 FLOPs를 차지하지만, 위의 요소들에 의해 지배되거나 융합(fused)됩니다.

다음 몇 섹션에서는 prefill과 generation의 맥락에서 이들 각각을 살펴보고 무엇이 우리의 성능에 병목이 될 가능성이 있는지 물어볼 것입니다. 단일 가속기 내에서, 우리는 compute-bound일까요 아니면 memory-bound일까요? 우리는 prefill과 generation에 대한 답이 얼마나 다를지 강조하고 싶습니다.

Linear operations: what bottlenecks us?

우리의 모든 선형 연산은 MLP 블록에 있든 어텐션에 있든 개념적으로 동일합니다. 그들의 arithmetic intensity는 배치 크기에 달려 있습니다. 섹션 1에서 이 수학을 다루었지만 반복할 가치가 있습니다. $\text{bf16[B, D]}$ 배치와 $\text{bf16[D, F]}$ 행렬의 단일 행렬 곱셈을 살펴봅시다. 이것은 큰 MLP 블록($W_\text{in}$ 또는 $W_\text{out}$)이거나 더 작은 어텐션 프로젝션($W_Q$, $W_K$, $W_V$, $W_O$) 중 하나일 수 있습니다. 이 matmul을 수행하려면 HBM에서 이 두 배열을 모두 MXU로 로드하고, 곱셈을 수행한 다음, 결과를 HBM에 다시 써야 합니다. 이전과 같이:

\(T_\text{math} = \frac{\text{Computation FLOPs}}{\text{Accelerator FLOPs/s}} = \frac{2BDF}{\text{Accelerator FLOPs/s}}\) \(T_\text{math} = \frac{\text{Computation FLOPs}}{\text{Accelerator FLOPs/s}} = \frac{2BDF}{\text{Accelerator FLOPs/s}}\)

\(T_\text{comms} = \frac{\text{Communication Bytes}}{\text{Bandwidth Bytes/s}} = \frac{2BD + 2FD + 2BF}{\text{Bandwidth Bytes/s}}\) \(T_\text{comms} = \frac{\text{Communication Bytes}}{\text{Bandwidth Bytes/s}} = \frac{2BD + 2FD + 2BF}{\text{Bandwidth Bytes/s}}\)

TPU나 GPU는 연산을 수행하면서 로드를 중첩할 수 있으므로, compute-bound가 되려면 \(T_\text{math} \geq T_\text{comms}\)가 필요합니다. 즉:

\(\frac{2BDF}{2BD + 2DF + 2BF} \geq \frac{\text{Accelerator FLOPs/s}}{\text{Bandwidth Bytes/s}} \underset{\text{TPU v5e}}{=} \frac{1.97E+14}{8.20E+11} = 240\) \(\frac{2BDF}{2BD + 2DF + 2BF} \geq \frac{\text{Accelerator FLOPs/s}}{\text{Bandwidth Bytes/s}} \underset{\text{TPU v5e}}{=} \frac{1.97E+14}{8.20E+11} = 240\)

여기서 RHS는 우리 하드웨어의 arithmetic intensity입니다. 이제 $D$와 $F$가 $B$에 비해 매우 크다고 가정하면(보통 배치는 최대 500이고 $D$와 $F > 10k$임), $\small{2BD + 2DF + 2BF \approxeq 2DF}$라는 사실을 사용하여 분모를 단순화할 수 있습니다.

\[\begin{align*} \frac{2BDF}{2BD + 2DF + 2BF} \approxeq \frac{2BDF}{2DF} \geq \frac{\text{Accelerator FLOPs/s}}{\text{Bandwidth Bytes/s}} \\ \underset{\text{TPU v5e}}{=} \frac{1.97E+14}{8.20E+11} \implies B \geq 240 = B_{\text{crit}} \frac{2BDF}{2BD + 2DF + 2BF} \approxeq \frac{2BDF}{2DF} \geq \frac{\text{Accelerator FLOPs/s}}{\text{Bandwidth Bytes/s}} \\ \underset{\text{TPU v5e}}{=} \frac{1.97E+14}{8.20E+11} \implies B \geq 240 = B_{\text{crit}} \end{align*}\]

가중치를 양자화하거나 행렬 곱셈에 더 낮은 정밀도의 FLOPs를 사용하면 이 임계 배치 크기가 변경될 수 있습니다. 예를 들어, 가중치를 int8 또는 fp8로 양자화하면 $B_\text{crit}$는 2배 감소합니다. FLOPs를 int8 또는 fp8로 수행하면 $B_\text{crit}$는 2배 증가합니다. 따라서 $\beta = \text{bits per param} / \text{bits per activation}$ 및 $\alpha_\text{hbm} = C / W_\text{hbm}$이라고 하면, 임계 배치 크기는 실제로 $B_\text{crit} = \beta \alpha_\text{hbm}$입니다.

Takeaway: Transformer matmul은 복제본당 토큰 배치 크기가 $B_\text{crit} = C / W_\text{hbm} \cdot (\text{bits per param} / \text{bits per activation}) = \beta \cdot \alpha_\text{hbm}$보다 클 때 오직 그때만 compute-bound입니다. TPU v5e의 bf16 활성화의 경우 이는 240 토큰입니다. H100의 경우 약 280 토큰입니다.

훈련 중에는 매우 큰 배치에 대해 동일한 가중치를 재사용하기 때문에 모든 행렬 곱셈 동안 높은 intensity를 갖게 됩니다. 이 높은 arithmetic intensity는 prefill로 이어집니다. 사용자 프롬프트는 일반적으로 수백, 수천 토큰 길이이기 때문입니다. 이전에 보았듯이 TPUv5e의 하드웨어 arithmetic intensity는 240이므로, 240 토큰보다 긴 시퀀스가 bf16에서 이 하드웨어의 밀집 모델에 공급되면 compute-bound가 될 것으로 예상할 수 있으며 모든 것이 잘 됩니다. 이보다 짧은 프롬프트는 기술적으로 더 높은 활용률을 달성하기 위해 함께 배치될 수 있지만, 일반적으로 필요하지 않습니다.

Takeaway: Prefill 중에는 모든 행렬 곱셈이 기본적으로 항상 compute-bound입니다. 따라서 하드웨어 활용률 또는 MFU(Model FLOPs Utilization)를 최대화하는 것만으로도 칩당 처리량(비용)과 지연 시간(TTFT 형태)을 최대화하기에 충분합니다. 프롬프트가 극히 짧지 않은 이상, 프롬프트별 수준에서의 배칭은 prefill 처리량의 작은 향상을 위해 지연 시간만 추가할 뿐입니다.

그러나 generation 중에는 각 요청에 대해 단계 간 순차적 의존성이 있기 때문에 한 번에 하나의 토큰만 순방향 패스를 수행할 수 있습니다! 따라서 여러 요청을 함께 배치하고 배치 차원에 걸쳐 병렬화해야만 (쉽게) 좋은 활용률을 달성할 수 있습니다. 나중에 더 이야기하겠지만, 지연 시간에 영향을 주지 않으면서 많은 동시 요청을 실제로 배칭하는 것은 어렵습니다. 그 때문에, generation으로 하드웨어 FLOPs를 포화시키는 것은 훨씬 더 어렵습니다.

Takeaway: Generation 중에는 선형/피드포워드 연산에서 compute-bound가 되려면 총 토큰 배치 크기가 $B_{\text{crit}}$보다 커야 합니다 (TPU v5e에서 bf16 파라미터의 경우 240). Generation은 토큰별로 직렬로 발생하므로, 이를 위해서는 여러 요청을 함께 배치해야 하며 이는 어렵습니다!

이것이 얼마나 큰지 주목할 가치가 있습니다! Generation 배치 크기 240은 한 번에 240개의 동시 요청을 생성하고 밀집 모델의 경우 240개의 별도 KV 캐시를 의미합니다. 즉, 일부 대량 추론 설정을 제외하고는 실제로 달성하기 어렵습니다. 반대로 prefill 중에 240개 이상의 토큰을 밀어넣는 것은 꽤 일상적이지만, 희소성이 증가함에 따라 약간의 주의가 필요합니다.

이 정확한 숫자는 양자화 및 하드웨어 종류에 따라 다를 수 있습니다. 가속기는 종종 더 낮은 정밀도에서 더 많은 산술 연산을 제공할 수 있습니다. 예를 들어, int8 파라미터를 가지고 있지만 bf16으로 계산하는 경우 임계 배치 크기는 120으로 떨어집니다. int8 활성화와 int8 파라미터를 사용하면 TPUv5e가 400 TOPs/s의 int8 x int8을 제공할 수 있으므로 다시 240으로 점프합니다.

What about attention?

내적 어텐션 연산을 살펴보면 상황이 더 복잡해지며, 특히 KV 캐시를 고려해야 합니다. 순수 멀티 헤드 어텐션이 있는 하나의 어텐션 헤드만 살펴보겠습니다. 단일 Flash Attention 융합에서 우리는여기서 softmax 적용, 마스크 등 matmul이 아닌 FLOPs를 무시하여 꽤 단순화했습니다. 계산이나 HBM 읽기와 중첩되어야 하지만 특정 TPU 세대에서는 수행하기가 까다로울 수 있습니다. 이러한 세부 사항은 KV 캐시가 일반적으로 memory bound라는 주요 메시지를 변경하지 않습니다.:

  1. HBM에서 모양이 $\text{bf16[B, T, D]}$인 $Q$ 활성화를 읽습니다.
  2. HBM에서 한 쌍의 $\text{bf16[B, S, D]}$ 텐서인 $KV$ 캐시를 읽습니다.
  3. \(QK\) matmul에서 $2BSTD$ FLOPs를 수행합니다. Flash Attention을 사용하면 $\text{bf16[B, S, T]}$ 어텐션 행렬을 HBM에 다시 쓸 필요가 없습니다.
  4. 어텐션 \(AV\) matmul에서 $2BSTD$를 수행합니다.
  5. 결과 $\text{bf16[B, T, D]}$ 텐서를 HBM에 다시 씁니다.

모두 합치면 다음과 같습니다:

\[\text{Multiheaded Attention Arithmetic Intensity} = \frac{4BSTD}{4BSD + 4BTD} = \frac{ST}{S+T}\]

Prefill의 경우, self-attention을 수행하므로 $S=T$이며, 이는 $T^2 / 2T = T / 2$로 단순화됩니다. 이는 prefill 중 어텐션의 arithmetic intensity가 $\Theta(T)$라는 것을 의미하므로 아주 좋습니다. 어텐션에 대해 compute-bound가 되기 꽤 쉽다는 뜻입니다. 시퀀스 길이가 꽤 길다면 괜찮을 것입니다!

하지만 generation은 사소한 시퀀스 차원을 가지고 $B$와 $D$ 차원이 상쇄되므로 다음과 같은 근사를 할 수 있습니다:

\[S \gg T = 1 \implies \frac{ST}{S+T} \approx 1\]

이것은 나쁩니다. generation 중 어텐션의 arithmetic intensity를 개선하기 위해 아무것도 할 수 없다는 것을 의미하기 때문입니다. 우리는 거대한 KV 캐시를 로드하면서 아주 적은 양의 FLOPs를 수행하고 있습니다. 따라서 어텐션 중에는 기본적으로 항상 메모리 대역폭 병목 상태입니다!

Takeaway: prefill 중에는 합리적인 시퀀스 길이(대략 $\gt 480$ 토큰)에 대해 어텐션이 보통 compute bound인 반면, generation 중에는 arithmetic intensity가 낮고 일정하므로 항상 메모리 대역폭 병목 상태입니다.

개념적으로 왜 그럴까요? 주로, 선형 부분에서 compute-bound인 이유는 파라미터(메모리 대역폭이 많은 구성 요소)가 많은 배치 항목에 재사용되기 때문입니다. 그러나 모든 배치 항목에는 고유한 KV 캐시가 있으므로 배치 크기가 클수록 KV 캐시가 더 많아집니다. 아키텍처가 공격적으로 조정되지 않는 한 여기서는 거의 항상 memory bound일 것입니다.

이는 또한 파라미터 메모리가 KV 캐시 메모리와 비슷해지면 배치 크기를 늘려도 처리량 증가가 줄어드는 수확 체감을 얻게 된다는 것을 의미합니다. 수확 체감이 당신에게 해를 끼치는 정도는 단일 시퀀스에 대한 파라미터 대 KV 캐시 바이트의 비율, 즉 대략 $2DF / SHK$ 비율에 달려 있습니다. $HK\approx D$이므로 이는 대략 $F$ 대 $S$(시퀀스 길이)의 비율에 달려 있습니다. 이는 또한 KV 캐시를 더 작게 만드는 아키텍처 수정에 따라 달라집니다(잠시 후에 자세히 설명하겠습니다).

Theoretical estimates for LLM latency and throughput

이 수학으로부터 최적화할 때 목표로 삼아야 할 단계 시간에 대한 꽤 좋은 경계를 얻을 수 있습니다. (참고: 독자가 이 전체 챕터에서 가져가야 할 것이 하나 있다면 바로 다음 내용입니다). Generation 중 작은 배치 크기(일반적임)의 경우, 어텐션과 MLP 블록 모두에서 메모리 대역폭 병목 상태라고 가정하여 단계당 지연 시간의 하한을 정할 수 있습니다:

\[\begin{equation*} \text{Theoretical Min Step Time} = \frac{\text{Batch Size} \times \text{KV Cache Size} + \text{Parameter Size}}{\text{Total Memory Bandwidth}} \end{equation*}\]

마찬가지로 처리량에 대해서도:

\[\begin{equation*} \text{Theoretical Max Tokens/s} = \frac{\text{Batch Size} \times \text{Total Memory Bandwidth}}{\text{Batch Size} \times \text{KV Cache Size} + \text{Parameter Size}} \end{equation*}\]

결국 배치 크기가 커짐에 따라 FLOPs가 파라미터 로딩을 지배하기 시작하므로 실제로는 더 일반적인 방정식이 있습니다:

\[\begin{align} \tiny \text{Theoretical Step Time (General)} = \underbrace{\frac{\text{Batch Size} \times \text{KV Cache Size}}{\tiny \text{Total Memory Bandwidth}}}_{\text{Attention (always bandwidth-bound)}} + \underbrace{\max\left(\frac{2 \times \text{Batch Size} \times \text{Parameter Count}}{\text{Total FLOPs/s}}, \frac{\text{Parameter Size}}{\text{Total Memory Bandwidth}}\right)}_{\tiny \text{MLP (can be compute-bound)}} \end{align}\]

여기서 어텐션 구성 요소(왼쪽)는 결코 compute-bound가 아니므로 FLOPs 루프라인이 필요하지 않습니다. 이것들은 대략적인 계산에 꽤 유용합니다. 예를 들어:

Pop Quiz: int8 및 bf16 FLOPs, 8192 컨텍스트 및 100 kB / token KV 캐시를 사용하는 TPU v5e 4x4 슬라이스에서 30B 파라미터 밀집 모델로부터 배치 크기 4 토큰으로 generate 단계를 수행하고 싶다고 가정해 봅시다. 이 작업의 지연 시간에 대한 합리적인 하한은 얼마인가요? 256 토큰 배치를 샘플링하고 싶다면 어떨까요?

답을 보려면 여기를 클릭하세요.

Answer: int8에서 파라미터는 30e9 바이트를 사용하고 주어진 사양으로 KV 캐시는 각각 100e3 * 8192 = 819MB를 사용합니다. 16개의 칩이 있으며, 각각 8.1e11 bytes/s 대역폭과 1.97e14 bf16 FLOPs/s를 가집니다. 위 방정식에서 배치 크기가 작으므로 단계 시간은 최소 (4 * 819e6 + 30e9) / (16 * 8.1e11) = 2.5 ms가 될 것으로 예상합니다. 256 토큰에서는 MLP 블록에 대한 compute-bound 영역에 잘 들어가므로 단계 시간은 대략 (256 * 819e6) / (16 * 8.1e11) + (2 * 256 * 30e9) / (16 * 1.97e14) = 21ms가 됩니다.

보시다시피 여기에는 처리량과 지연 시간 사이에 명확한 트레이드오프가 있습니다. 작은 배치는 빠르지만 하드웨어를 잘 활용하지 못합니다. 큰 배치는 느리지만 효율적입니다. 다음은 일부 구형 PaLM 모델에 대해 계산된 지연 시간-처리량 파레토 프런티어입니다(ESTI 논문에서 발췌):

Figure: 여러 PaLM 모델에 대한 비용(읽기: 처리량) 대 지연 시간의 파레토 프런티어. 칩 수(C)와 배치 크기(B)가 파레토 프런티어를 따라 이동시키는 방법에 주목하세요. 단, 사용 가능한 메모리가 좋은 배치 크기를 지원하지 못해 처리량이 저하된 녹색 점(PaLM 540B용 C:32 B:16)은 예외입니다. 배치 크기 240 이후에는 처리량이 일반적으로 평평해지는 경향이 있음에 유의하세요. int8 가중치는 더 나은 지연 시간-처리량 파레토 최적을 제공하지만 더 나은 최대 처리량을 제공하지는 않습니다.

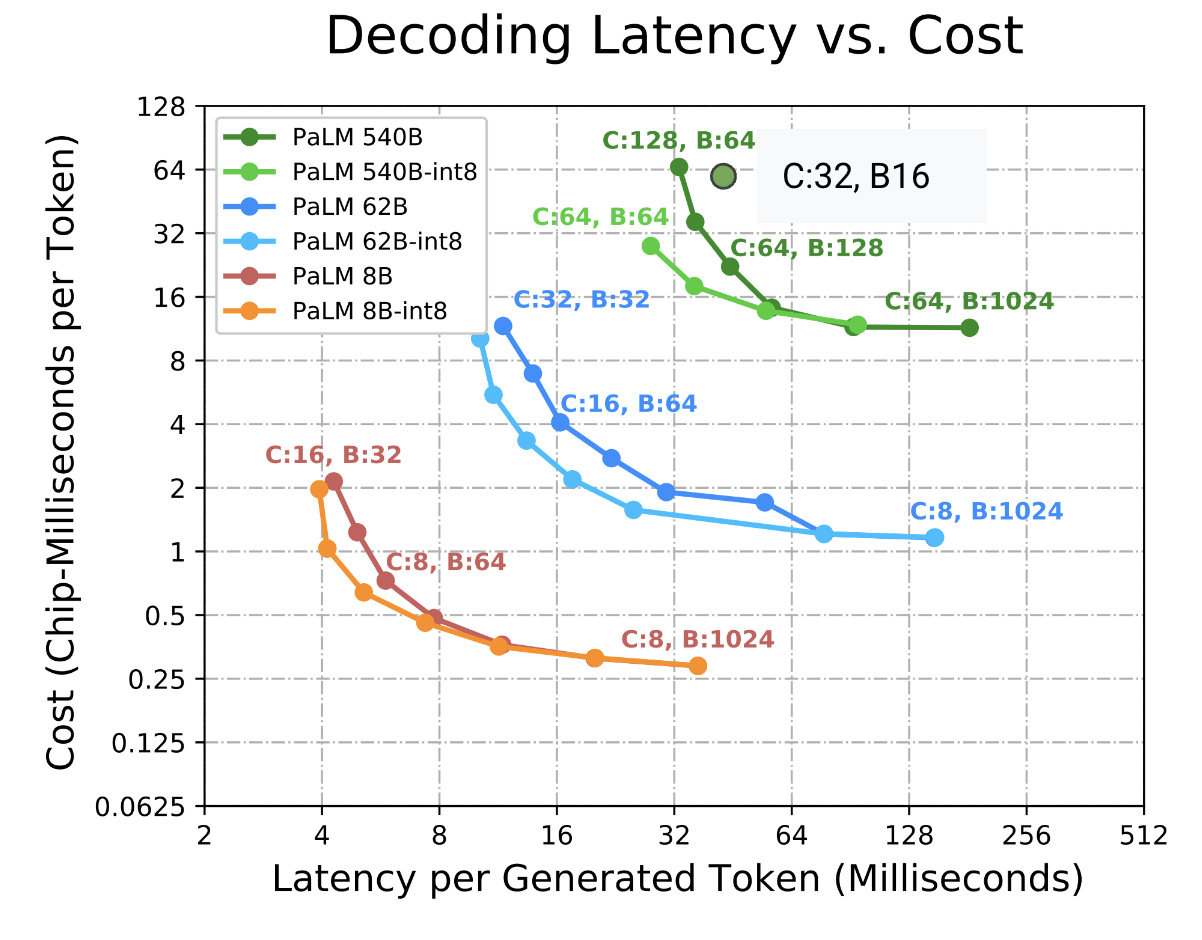
배치 크기를 조절하여 지연 시간과 처리량을 트레이드오프할 뿐만 아니라, HBM에 의해 제한되는 경우 더 큰 배치를 맞추기 위해 작은 토폴로지보다 더 큰 토폴로지를 선호할 수도 있습니다. 다음 섹션에서 이에 대해 자세히 살펴봅니다.

Takeaway: generation 처리량에 관심이 있다면 가능한 가장 큰 칩당 배치 크기를 사용하세요. TPU arithmetic intensity($B_\text{crit}$, 보통 120 또는 240) 이상의 칩당 배치 크기는 처리량을 최대화합니다. 이를 달성하기 위해 토폴로지를 늘려야 할 수도 있습니다. 더 작은 배치 크기는 처리량을 희생하여 지연 시간을 개선할 수 있게 해줍니다.

하드웨어 관점에서 이에 대한 몇 가지 주의 사항이 있습니다. 자세한 내용을 보려면 여기를 클릭하세요.

이것은 모두 상당히 이론적입니다. 실제로는 다음과 같은 몇 가지 이유로 날카로운 루프라인을 잘 보지 못합니다:

  • HBM 읽기가 FLOPs와 완벽하게 중첩될 것이라는 가정은 비현실적입니다. 우리의 컴파일러(XLA)는 오류가 있기 때문입니다.
  • 샤딩된 모델의 경우, XLA는 종종 모델 샤딩된 행렬 곱셈의 ICI 통신을 FLOPs 자체와 효율적으로 중첩하지 못하므로 \(\text{BS}=32\) 이상의 선형 연산에서 지연 시간 타격을 입기 시작하는 경우가 많습니다.
  • 이론적 루프라인보다 큰 배치 크기는 불완전한 중첩으로 인해 여전히 처리량 향상을 볼 수 있지만, 이것은 좋은 휴리스틱입니다.

What about memory?

대역폭과 FLOPs를 살펴보는 데 시간을 보냈지만 메모리는 살펴보지 않았습니다. 추론 시 메모리 상황은 새로운 데이터 구조인 KV 캐시 덕분에 훨씬 다르게 보입니다. 이 섹션에서는 상황이 얼마나 다른지 보여주기 위해 실제 모델(LLaMA 2-13B)을 선택해 보겠습니다:

hyperparam value
L (num_layers) 40
D (d_model) 5,120
F (ffw_dimension) 13,824
N (num_heads) 40
K (num_kv_heads) 40
H (qkv_dim) 128
V (num_embeddings) 32,000

추론 중에 메모리를 사용하는 것은 무엇일까요? 당연히 파라미터입니다. 이를 계산하면 다음과 같습니다:

param formula size (in bytes)
FFW params d_model2 x ffw_multiplier x 3 (for gelu + out-projection) x n_layers 5,120 x 5,120 x 2.7 x 3 x 40 = 8.5e9
Vocab params 2 (input and output embeddings) x n_embeddings x d_model 2 x 32,000 x 5,120 = 0.3e9
Attention params [2 (q and output) x d_model x n_heads x d_qkv + 2 (for k and v) x d_model x n_kv_heads x d_qkv] x n_layers (2 x 5,120 x 40 x 128 + 2 x 5,120 x 40 x 128) x 40 = 4.2e9

이 파라미터들을 더하면 예상대로 8.5e9 + 4.2e9 + 0.3e9 = 13e9 총 파라미터를 얻습니다. 이전 섹션에서 보았듯이 훈련 중에는 float32의 옵티마이저 상태와 함께 bfloat16에 파라미터를 저장할 수 있습니다. 이는 약 100GB의 메모리를 사용할 수 있습니다. 이는 수 TB를 사용할 수 있는 그라디언트 체크포인트에 비하면 새발의 피입니다.

추론은 어떻게 다른가요? 추론 중에는 파라미터의 복사본 하나를 저장하는데, 예를 들어 bfloat16이라고 합시다. 이는 26GB를 사용하며 실제로 양자화를 통해 이보다 훨씬 더 잘할 수 있는 경우가 많습니다. 추적해야 할 옵티마이저 상태나 그라디언트가 없습니다. 체크포인트를 하지 않기 때문에(역방향 패스를 위해 활성화를 유지하지 않음), 활성화 사용량은 prefill특히 어텐션 행렬 구체화를 피하는 Flash Attention 덕분에과 generate 모두에 대해 무시할 수 있습니다. 8k 토큰을 prefill하면 단일 활성화는 8,192 x 5,120 x 2 bytes = 80MB의 메모리만 사용합니다. 더 긴 prefill은 많은 더 작은 순방향 패스로 나눌 수 있으므로 더 긴 컨텍스트에서도 문제가 되지 않습니다. Generation은 그보다 더 적은 토큰을 사용하므로 활성화는 무시할 수 있습니다.

주요 차이점은 KV 캐시입니다. 이는 모든 과거 토큰에 대한 키 및 값 프로젝션이며, 최대 허용 시퀀스 길이에 의해서만 크기가 제한됩니다. \(T\) 토큰에 대한 총 크기는 다음과 같습니다.

\[\text{KV cache size} = 2 \cdot \text{bytes per float} \cdot H \cdot K \cdot L \cdot T\]

여기서 \(H\)는 각 헤드의 차원, \(K\)는 KV 헤드의 수, \(L\)은 레이어 수이며, 2는 키와 값을 모두 저장하는 것에서 나옵니다.

이는 매우 빠르게 커질 수 있습니다, 적당한 배치 크기와 컨텍스트 길이에서도 말이죠. LLaMA-13B의 경우 bf16에서 단일 8192 시퀀스에 대한 KV 캐시는

\[8192\ (T) \times 40\ (K) \times 128\ (H) \times 40\ (L) \times 2\ (\text{bytes}) \times 2 = 6.7 \text{GB}\]

이 중 4개만으로도 파라미터의 메모리 사용량을 초과합니다! 분명히 말씀드리면, LLaMA 2는 긴 컨텍스트에서 KV 캐시 크기에 최적화되지 않았습니다(LLaMA-3처럼 일반적으로 $K$가 훨씬 작기 때문에 항상 이렇게 나쁜 것은 아닙니다). 하지만 이는 여전히 설명이 됩니다. 메모리 또는 지연 시간 추정에서 이를 무시할 수 없습니다.

Modeling throughput and latency for LLaMA 2-13B

최대 이론적 처리량을 위해 이전에 도출된 임계 배치 크기(240)까지 8xTPU v5es에서 다양한 배치 크기로 generation을 완벽하게 효율적으로 수행하려고 하면 어떻게 되는지 살펴봅시다.

Batch Size 1 8 16 32 64 240
KV Cache Memory (GiB) 6.7 53.6 107.2 214.4 428.8 1608
Total Memory (GiB) 32.7 79.6 133.2 240.4 454.8 1634
Theoretical Step Time (ms) 4.98 12.13 20.30 36.65 69.33 249.09
Theoretical Throughput (tokens/s) 200.61 659.30 787.99 873.21 923.13 963.53

8x TPU v5es는 128GiB의 HBM, 6.5TiB/s의 HBM 대역폭(각각 0.82TiB/s) 및 1600TF/s의 컴퓨팅을 제공합니다.

이 모델의 경우 배치 크기를 늘리면 처리량이 향상되지만 급격한 수확 체감을 겪습니다. 배치 크기 16을 넘어가면 OOM(Out Of Memory)이 발생하며 240에 근접하려면 훨씬 더 많은 메모리가 필요합니다. 더 큰 토폴로지는 지연 시간을 개선할 수 있지만 칩당 처리량의 벽에 부딪혔습니다.

총 파라미터 수는 그대로 유지하지만 마법처럼 KV 캐시를 5배 더 작게 만든다고 가정해 봅시다(예: 1:5 GMQA, 즉 40개의 Q 헤드에 대해 8개의 KV 헤드를 공유함 - 자세한 내용은 다음 섹션 참조).

Batch Size 1 8 16 32 64 240
KV Cache Memory (GiB) 1.34 10.72 21.44 42.88 85.76 321.6
Total Memory (GiB) 27.34 36.72 47.44 68.88 111.76 347.6
Theoretical Step Time (ms) 4.17 5.60 7.23 10.50 17.04 52.99
Theoretical Throughput (tokens/s) 239.94 1,429.19 2,212.48 3,047.62 3,756.62 4,529.34

더 작은 KV 캐시로도 여전히 수확 체감이 있지만, 칩당 이론적 처리량은 배치 크기 240까지 계속 확장됩니다. 훨씬 더 큰 배치 64를 수용할 수 있으며 지연 시간도 모든 배치 크기에서 일관되게 더 좋습니다. 지연 시간, 최대 처리량, 최대 배치 크기가 모두 획기적으로 향상되었습니다! 사실, 이후의 LLaMA 세대는 이 최적화를 정확히 사용했습니다. LLaMA-3 8B는 32개의 쿼리 헤드와 8개의 KV 헤드를 가지고 있습니다 (출처).

Takeaway: 파라미터 외에도 KV 캐시의 크기는 모델의 궁극적인 추론 성능에 많은 영향을 미칩니다. 우리는 아키텍처 결정과 런타임 최적화의 조합으로 이를 통제하고 싶습니다.

Tricks for Improving Generation Throughput and Latency

원본 Attention is All You Need 논문 이후, 모델을 더 효율적으로 만들기 위한 많은 기술이 개발되었으며, 종종 KV 캐시를 구체적으로 목표로 합니다. 일반적으로 KV 캐시가 작으면 지연 시간을 해치지 않으면서 generation 단계의 배치 크기와 컨텍스트 길이를 늘리기가 더 쉬워지고, Transformer를 둘러싼 시스템(예: 요청 캐싱)의 작업이 더 쉬워집니다. 품질에 미치는 영향은 무시하고 살펴보면 다음과 같습니다:

Grouped multi-query attention (aka GMQA, GQA): KV 헤드의 수를 줄이고 어텐션 메커니즘에서 많은 Q 헤드와 공유할 수 있습니다. 극단적인 경우 단일 KV 헤드를 모든 Q 헤드에 공유할 수 있습니다. 이는 순수 MHA에 비해 Q:KV 비율만큼 KV 캐시를 줄이며, 모델의 성능이 이러한 변화에 비교적 둔감하다는 것이 관찰되었습니다.

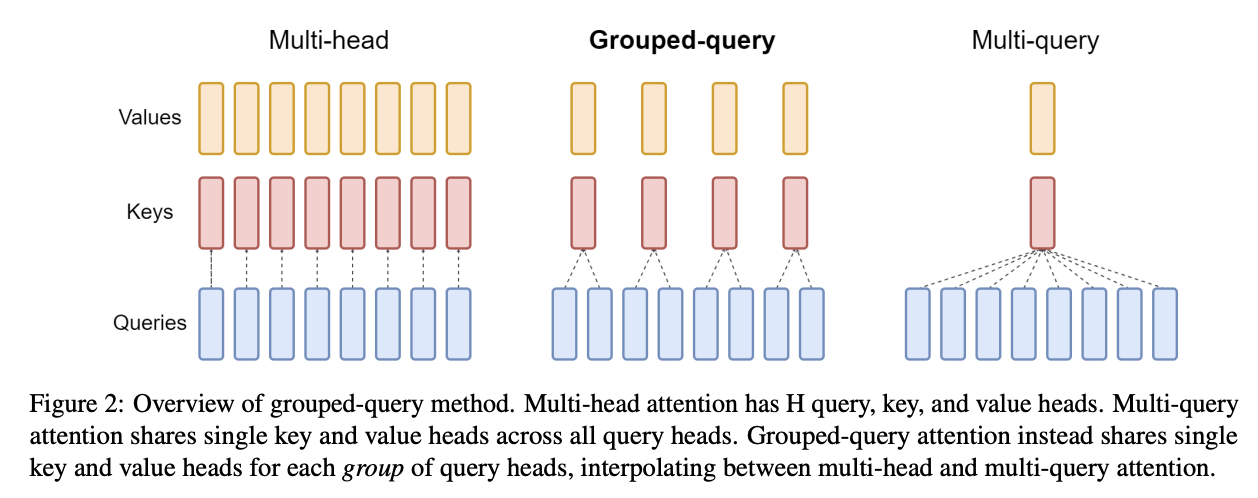
이는 또한 어텐션 계산의 arithmetic intensity를 효과적으로 증가시킵니다 (섹션 4의 질문 4 참조).

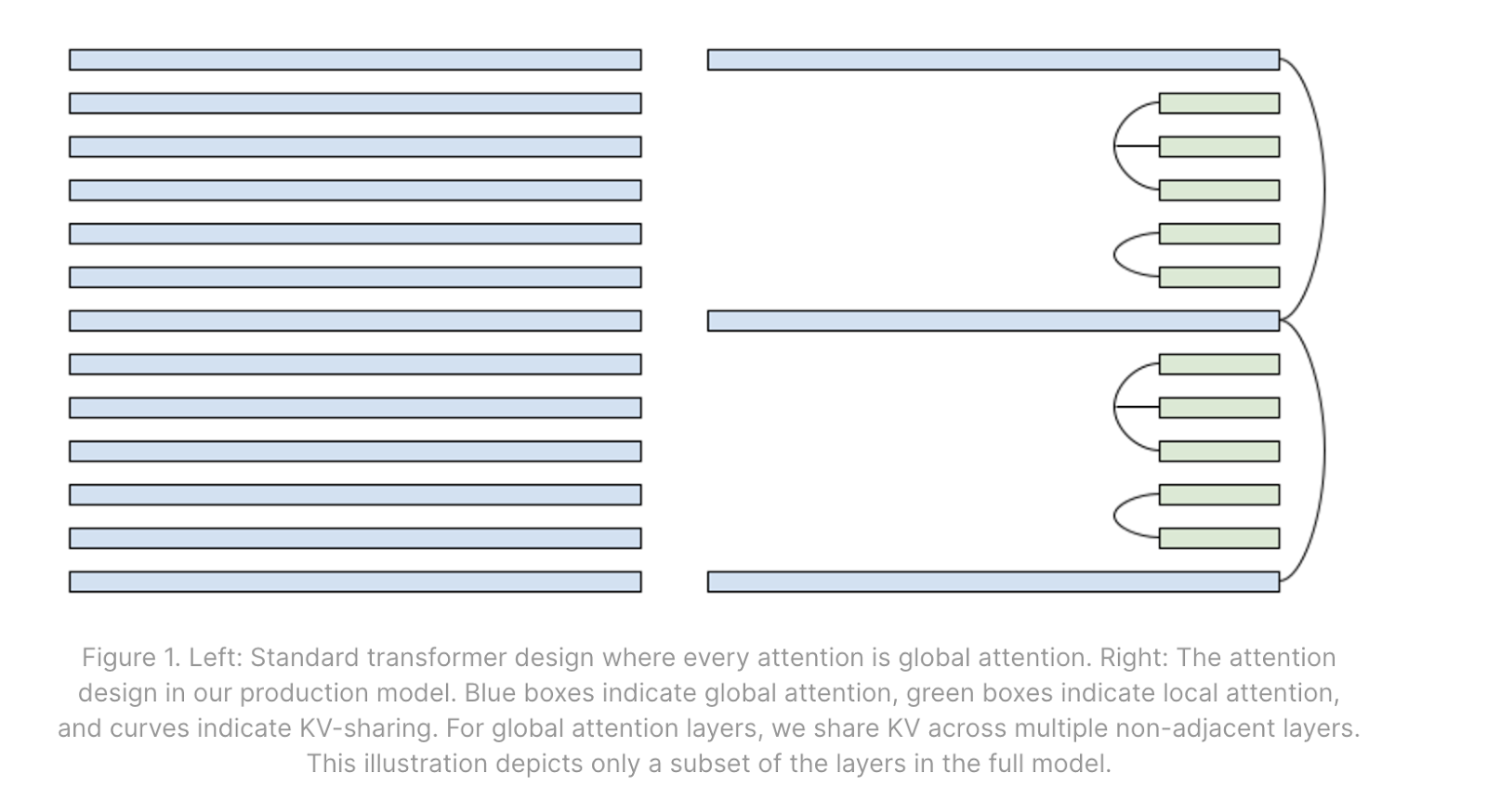
Mixing in some local attention layers: Local attention은 컨텍스트를 작거나 중간 크기의 최대 길이로 제한합니다. 훈련 및 prefill 시간에 이는 어텐션 행렬을 삼각형 대신 대각선 띠로 마스킹하는 것을 포함합니다. 이것은 로컬 레이어에 대한 KV 캐시의 최대 길이를 효과적으로 제한합니다. 모델에 일부 로컬 레이어를 일부 글로벌 레이어와 혼합함으로써, 로컬 윈도우보다 긴 컨텍스트에서 KV 캐시가 크게 줄어듭니다.

Sharing KVs across layers: 모델은 어떤 패턴으로 레이어 간에 동일한 KV 캐시를 공유하도록 학습될 수 있습니다. 이는 KV 캐시 크기를 줄이고 배치 크기 증가, 캐싱, 오프라인 저장 등의 이점을 제공하지만, 공유된 KV 캐시는 HBM에서 여러 번 읽어야 할 수 있으므로 반드시 단계 시간을 개선하는 것은 아닙니다.

왼쪽: 순수 글로벌 어텐션의 다중 레이어. 오른쪽: 인접 레이어와 공유하는 일부 글로벌/로컬 인터리빙 패턴의 예. 출처: Character.ai 블로그.

Quantization: 추론은 일반적으로 파라미터와 KV의 정밀도에 덜 민감합니다. 파라미터와 KV 캐시를 양자화(예: int8, int4, fp8 등)함으로써 두 가지 모두에서 메모리 대역폭을 절약하고, compute roofline에 도달하는 데 필요한 배치 크기를 줄이고, 더 큰 배치 크기에서 실행할 메모리를 절약할 수 있습니다. 양자화는 모델이 양자화로 훈련되지 않았더라도 훈련 후에 종종 적용될 수 있다는 추가적인 장점이 있습니다.

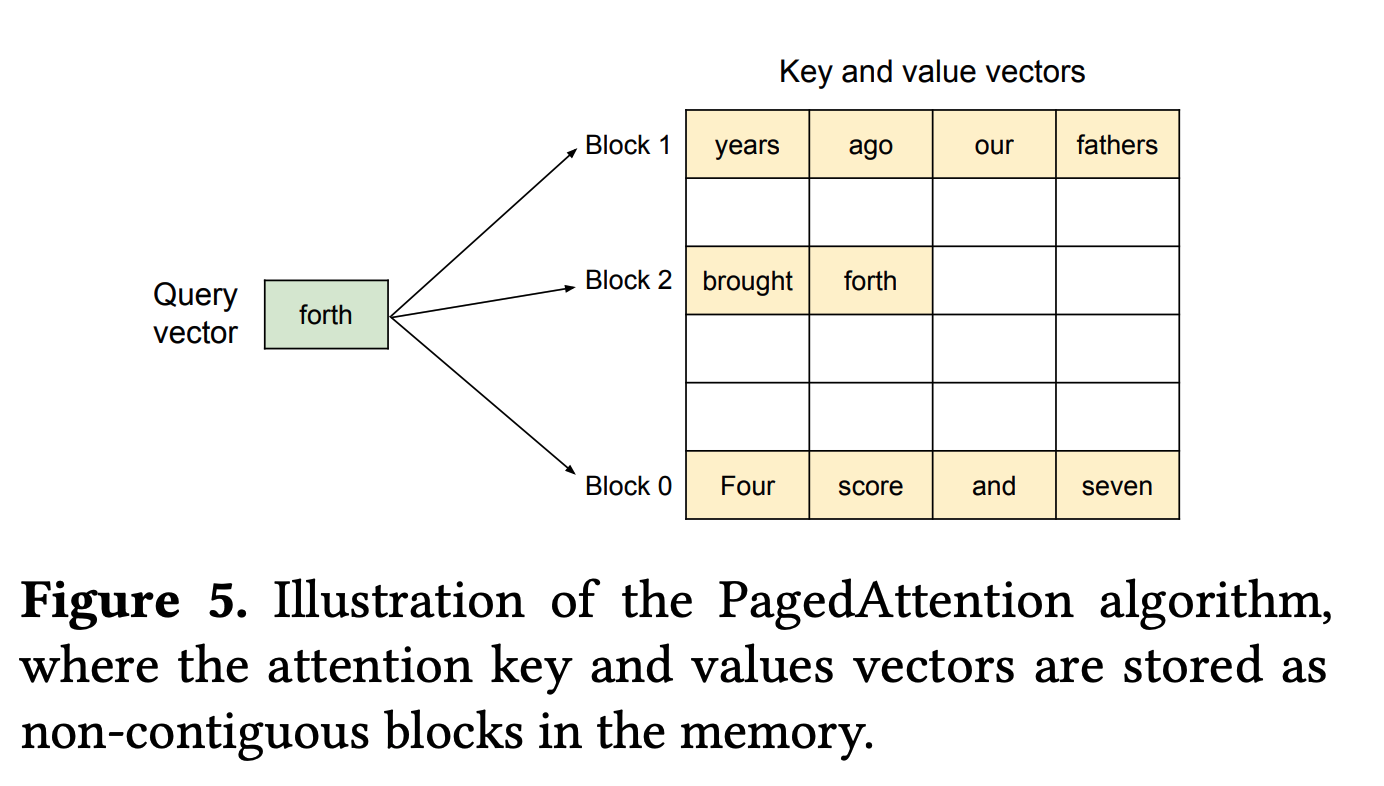
Using ragged HBM reads and Paged Attention: 위의 계산에서는 각 KV 캐시에 대해 8k 컨텍스트를 할당했지만, 전체 KV 캐시를 메모리에서 읽을 필요는 없는 경우가 많습니다. 요청은 다양한 길이 분포를 가지며 모델의 최대 컨텍스트를 사용하지 않으므로, KV 캐시의 패딩이 아닌 부분만 읽는 커널(예: Flash Attention 변형)을 종종 구현할 수 있습니다.

Paged Attention은 KV 캐시를 OS 스타일 페이지 테이블에 저장하고 KV 캐시 패딩을 대부분 피하는 이에 대한 개선입니다. 이는 복잡성을 많이 추가하지만 모든 배치가 필요한 만큼의 메모리만 사용한다는 것을 의미합니다. 이것은 런타임 최적화이므로 아키텍처와 무관합니다.

Figure: generation 중 단일 토큰(네 번째)이 여러 KV 캐시 블록/페이지에 주의를 기울입니다. KV 캐시를 페이징함으로써 필요 이상의 메모리를 로드하거나 저장하는 것을 방지합니다. PagedAttention 논문에서 발췌.

Big Picture: 이 모든 것을 종합하면, 이러한 KV 캐시 최적화는 표준 MHA Transformer에 비해 KV 캐시 크기를 10배 이상 줄일 수 있습니다. 이는 Transformer의 전체 비용을 10배 개선하는 결과를 가져올 수 있습니다.

Distributing Inference Over Multiple Accelerators

지금까지는 단일 칩을 넘어 확장하는 방법을 대충 넘겼습니다. 섹션 5에 이어, 사용 가능한 다양한 전략과 트레이드오프를 살펴보겠습니다. 언제나 그렇듯 prefill과 generation을 별도로 살펴보겠습니다.

Prefill

루프라인 관점에서 prefill은 훈련과 거의 동일하며 거의 모든 동일한 기술과 트레이드오프가 적용됩니다. 모델(Megatron) 병렬 처리, 시퀀스 샤딩(충분히 긴 컨텍스트의 경우), 파이프라이닝, 심지어 FSDP도 모두 실행 가능합니다! 나중에 generation을 수행할 수 있도록 KV를 계속 유지하기만 하면 됩니다. 훈련과 마찬가지로 칩 수를 늘리면 더 많은 FLOPs/s에 액세스할 수 있지만(잠재적으로 더 낮은 TTFT를 위해), 통신 오버헤드가 추가됩니다(잠재적으로 칩당 처리량 감소).

The general rule for sharding prefill: 다음은 prefill에 대한 일반적인 규칙 세트입니다. 단일 시퀀스에 대해서만 prefill을 수행한다고 가정합니다(배치 차원 없음):

  1. Model sharding: 일반적으로 ICI-bound가 되는 지점까지 일정량의 모델 병렬 처리를 먼저 수행합니다. 섹션 5에서 보았듯이 이는 1축에 대해 $F / 2200$ 정도입니다(보통 약 4-8방향 샤딩).
  2. Sequence parallelism: 이 외에는 시퀀스 병렬 처리(데이터 병렬 처리와 같지만 시퀀스 차원에 걸쳐 샤딩함)를 수행합니다. 시퀀스 병렬 처리는 어텐션에서 약간의 추가 통신을 도입하지만, 긴 컨텍스트에서는 일반적으로 상당히 작습니다. 훈련과 마찬가지로 통신과 계산을 중첩시킬 수 있습니다(각각 collective matmul과 ring attention 사용).

Takeaway: prefill 중에는 훈련 중에 작동할 수 있는 거의 모든 샤딩이 잘 작동합니다. ICI 한계까지 모델 병렬 처리를 수행한 다음 시퀀스 병렬 처리를 수행하세요.

Generation

Generation은 prefill보다 더 복잡한 야수입니다. 우선, 많은 요청을 함께 배치해야 하므로 큰 배치 크기를 얻기가 더 어렵습니다. 지연 시간 목표는 더 낮습니다. 이로 인해 일반적으로 더 memory-bound이고 통신 오버헤드에 더 민감하여 샤딩 전략이 제한됩니다:

  1. FSDP is impossible: 파라미터와 KV 캐시를 HBM에서 MXU로 로드하는 데 있어 memory-bound이므로, HBM보다 몇 배나 느린 ICI를 통해 이동시키고 싶지 않습니다. 우리는 가중치가 아닌 활성화를 이동시키고 싶습니다. 이는 FSDP와 유사한 방법이 generation에는 일반적으로 완전히 실행 불가능함을 의미합니다.훈련 후 실수로 켜두는 것은 10배 정도의 성능 저하를 겪는 쉽고 흔한 방법입니다

  2. There is no reason to do data parallelism: 순수 데이터 병렬 처리는 파라미터를 복제하고 파라미터를 더 빨리 로드하는 데 도움이 되지 않으므로 도움이 되지 않습니다. 대신 모델의 여러 사본을 띄우는 것이 더 낫습니다.이것은 모델의 사본이 있는 여러 서버를 더 작은 배치 크기로 띄운다는 것을 의미합니다. 모델 수준에서의 데이터 병렬 처리는 엄밀히 더 나쁩니다.

  3. No sequence = no sequence sharding. 시퀀스 샤딩은 불가능합니다.

이것은 밀집 모델 generation을 위한 모델 샤딩의 변형을 주로 남깁니다. prefill과 마찬가지로 우리가 할 수 있는 가장 간단한 것은 간단한 모델 병렬 처리(활성화 완전 복제, MLP의 히든 차원에 대해 가중치 완전 샤딩)이며, ICI 제한이 될 때까지 최대 4-8방향입니다. 그러나 종종 메모리 대역폭 제한이 있기 때문에 실제로 이 한계를 넘어 지연 시간을 개선할 수 있습니다!

Note on ICI bounds for generation: 훈련 중에는 compute-bound가 되기를 원하므로 루프라인은 ICI 통신이 FLOPs보다 오래 걸리는 시점을 봅니다. 그러나 generation 중에는 파라미터 로딩에 의해 메모리 대역폭 제한이 있는 경우, 처리량 비용(tokens/sec/chip 측면에서)을 최소화하면서 이 지점 이상으로 모델 샤딩을 늘리고 지연 시간을 개선할 수 있습니다. 더 많은 모델 샤딩은 가중치를 로드할 더 많은 HBM을 제공하며 FLOPs는 중요하지 않습니다.FLOPs 시간이 병목 현상을 일으키지 않는다는 의미에서, 우리가 걱정해야 할 것은 ICI 시간이 파라미터 로딩 시간을 초과하는 것입니다. 병목 현상이 되기 전에 얼마나 많은 모델 병렬 처리를 할 수 있는지 살펴봅시다.

\[\begin{align*}T_\text{HBM comms} = \frac{2DF}{Y \cdot W_\text{hbm}} && T_\text{ICI comms} = \frac{2BD}{W_\text{ici}}\end{align*}\] \[T_\text{ICI comms} > T_\text{HBM comms} \rightarrow \frac{W_\text{hbm}}{W_\text{ici}} > \frac{F}{Y \cdot B} \rightarrow Y > F / (B \cdot \beta)\]

여기서 $\beta = W_\text{hbm} / W_\text{ici}$입니다. 이 숫자는 TPU v5e 및 TPU v6e의 경우 일반적으로 약 8입니다. 즉, 예를 들어 $F$가 16,384이고 $B$가 32이면 이론적으로 의미 있는 처리량 타격 없이 최대 16384 / (32 * 8) = 64방향까지 모델 병렬 처리를 수행할 수 있습니다. 이는 KV 캐시를 64방향으로 완전히 샤딩할 수 있다고 가정하는 것인데, 이는 어렵습니다. 이에 대해서는 아래에서 논의합니다.

어텐션 레이어의 경우 \(W_Q\)와 \(W_O\)를 헤드에 대해 Megatron 스타일로 모델 샤딩합니다. KV 가중치는 매우 작으므로 $K$-방향 샤딩 이상으로 샤딩하는 것보다 복제하는 것이 종종 더 저렴합니다.

Takeaway: generation 중 유일한 옵션은 모델 병렬 처리의 변형입니다. 우리는 더 큰 KV 캐시나 파라미터 대신 활성화를 이동시키는 것을 목표로 합니다. 배치 크기가 클 때 FLOPs-ICI 한계($F / \alpha$)까지 모델 병렬 처리를 수행합니다. 배치 크기가 작을 때 더 많은 모델 샤딩을 통해 지연 시간을 개선할 수 있습니다(적당한 처리량 비용으로). KV 헤드보다 더 많은 방향으로 모델 샤딩을 하고 싶을 때 배치 차원을 따라 KV를 샤딩할 수도 있습니다.

Sharding the KV cache

우리는 또한 샤딩해야 할 추가 데이터 구조인 KV 캐시를 가지고 있습니다. 다시 말하지만, 캐시는 어텐션 지연 시간의 주요 원인이므로 복제하는 것을 거의 항상 피하고 싶습니다. 이를 위해 먼저 헤드 차원을 따라 KV를 Megatron-shard합니다. 이는 $K$-방향 샤딩으로 제한되므로 헤드 수가 적은 모델의 경우 헤드 차원을 가능한 한 많이 샤딩한 다음 배치 차원을 따라 샤딩합니다. 즉, $\text{KV}[2, B_Z, S, K_Y, H]$. 이는 KV 캐시가 완전히 분산됨을 의미합니다.

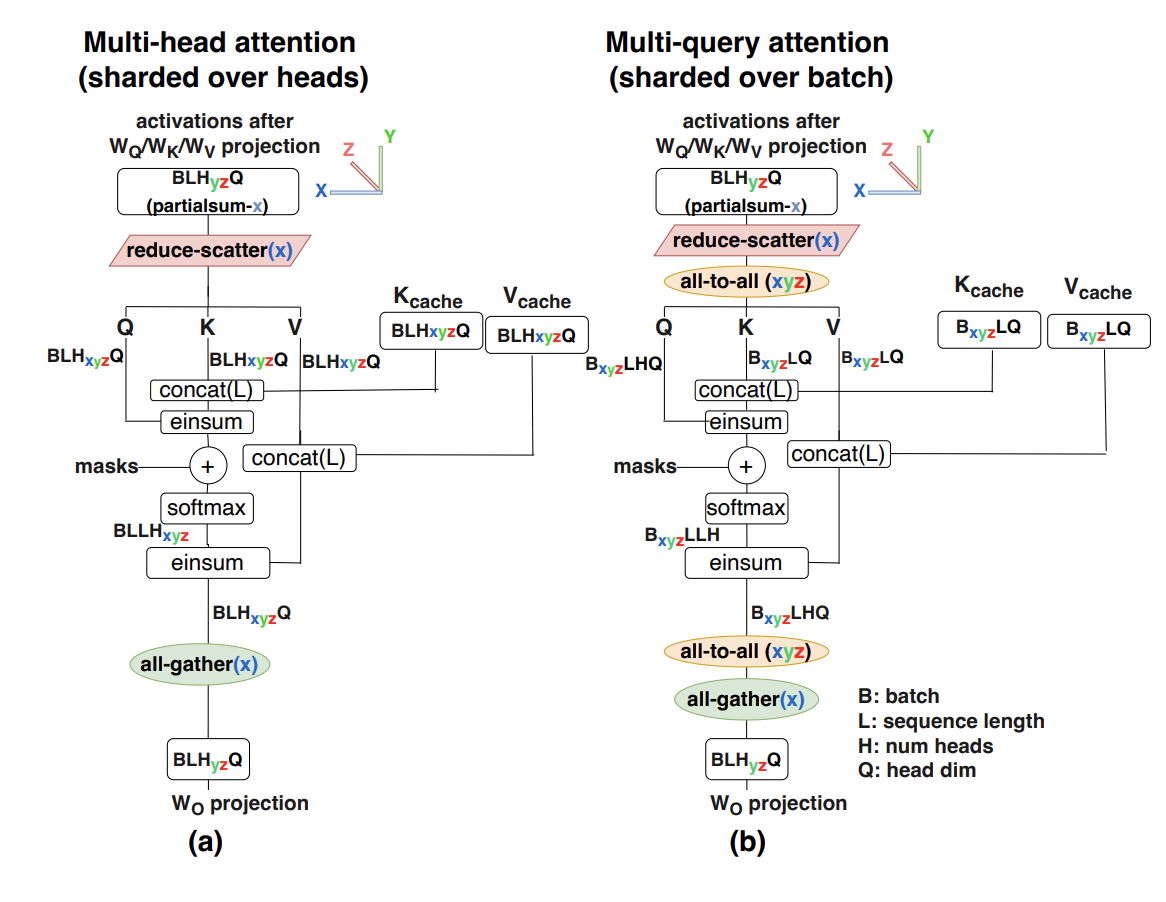
Figure: (a) 순수 모델 샤딩을 사용한 멀티 헤드 어텐션과 (b) KV 캐시의 배치 샤딩을 사용한 멀티쿼리 어텐션의 비교. KV 캐시에 작용할 수 있도록 활성화를 모델 샤딩에서 배치 샤딩으로 이동시키기 위해 두 개의 추가 AllToAll이 필요한 방식에 주목하세요.

이 비용은 어텐션 레이어마다 두 번의 AllToAll입니다 — 하나는 Q 활성화를 배치 샤딩으로 이동하여 배치 샤딩으로 어텐션을 계산할 수 있도록 하는 것이고, 하나는 배치 샤딩된 어텐션 출력을 다시 순수 모델 샤딩으로 이동시키는 것입니다.

여기에 전체 알고리즘이 있습니다!

여기서는 $Y$와 $Z$ 모두에 대해 모델 병렬 처리를 사용하는 전체 어텐션 알고리즘을 작성하겠습니다. 키 텐서와 KV 헤드 차원 모두에 $K$를 사용하여 죄송합니다. $M=N/K$라고 합시다.

  1. X[B, D] = … (기존 활성화, 이전 레이어에서 샤딩되지 않음)
  2. K[BZ, S, KY, H], V[BZ, S, K, H] = … (기존 KV 캐시, 배치 샤딩됨)
  3. Q[B, NYZ, H] = X[B, D] * WQ[D, NYZ, H]
  4. Q[BZ, NY, H] = AllToAllZ->B(Q[B, NYZ, H])
  5. Q[BZ, KY, M, H] = Reshape(Q[BZ, NY, H])
  6. O[BZ, S, KY, M] = Q[BZ, KY, M, H] *H K[BZ, S, KY, H]
  7. O[BZ, S, K, M] = SoftmaxS(O[BZ, S, KY])
  8. O[BZ, KY, M, H] = O[BZ, S, K, M] *S V[BZ, S, KY, H]
  9. O[B, KY, MZ, H] = AllToAllZ->M(O[BZ, KY, M, H])
  10. O[B, NYZ, H] = Reshape(O[B, KY, MZ, H])
  11. X[B, D] {UYZ} = WO[NYZ, H, D] *N,H O[B, NYZ, H]
  12. X[B, D] = AllReduce(X[B, D] { UYZ})

꽤 복잡하지만 일반적으로 어떻게 작동하는지 볼 수 있습니다. 새로운 통신은 작은 활성화에 작용하므로 적당히 비싼 반면, 그 대가로 KV(고정되어 있음)를 로드하는 막대한 양의 메모리 대역폭을 절약합니다.

Designing an Effective Inference Engine

지금까지 우리는 개별 prefill 및 generate 작업을 격리하여 효율적으로 최적화하고 샤딩하는 방법을 살펴보았습니다. 실제로 이를 효과적으로 사용하려면 지연 시간/처리량 파레토 프런티어에서 우리가 선택한 지점에 이 두 작업을 공급할 수 있는 추론 엔진을 설계해야 합니다.

가장 간단한 방법은 단순히 prefill 배치를 실행한 다음 generation 배치를 실행하는 것입니다:

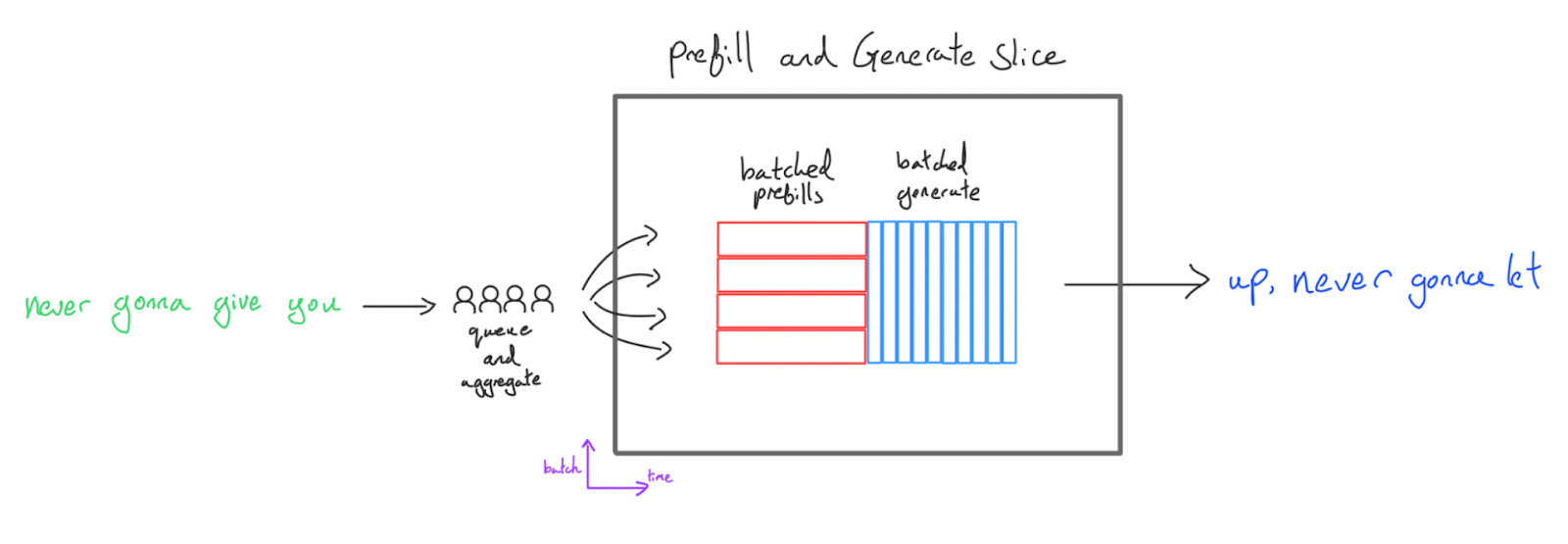
Figure: 가장 간단한 설정에서 요청이 집계되고, 서버는 prefill 배치를 실행하고 모든 시퀀스가 완료될 때까지 generate 함수를 호출하는 것을 번갈아 수행합니다.

이것은 구현하기 쉽고 대부분의 코드베이스에서 첫 번째 추론 설정이지만 여러 단점이 있습니다:

  1. 지연 시간이 끔찍합니다. prefill과 generate 배치 크기를 결합합니다. Time to first token (TTFT)은 큰 prefill 배치 크기에서 끔찍합니다 — 사용자가 토큰을 볼 수 있기 전에 모든 prefill을 완료해야 합니다. Generate 처리량은 작은 배치 크기에서 끔찍합니다.
  2. 더 긴 생성에 짧은 생성을 차단합니다. 많은 시퀀스가 다른 시퀀스보다 먼저 완료되어 generation 중에 빈 배치 슬롯을 남겨 generate 처리량을 더욱 해칩니다. 배치 크기와 generation 길이가 증가함에 따라 문제가 악화됩니다.
  3. Prefill이 패딩됩니다. Prefill은 가장 긴 시퀀스에 패딩되며 많은 컴퓨팅을 낭비합니다. 이에 대한 해결책이 있지만 역사적으로 XLA는 이러한 FLOPs를 건너뛰기가 꽤 어려웠습니다. 이것도 배치 크기와 prefill 시퀀스 길이가 클수록 더 나빠집니다.
  4. Prefill과 generation 간에 샤딩을 공유해야 합니다. Prefill과 generate 모두 동일한 슬라이스에 있으므로 둘 다에 대해 동일한 토폴로지와 샤딩을 사용하며(가중치 사본을 두 개 유지하지 않는 한), 이는 일반적으로 성능에 도움이 되지 않습니다(예: generate는 훨씬 더 많은 모델 샤딩을 원함).

따라서 이 방법은 에지 애플리케이션(보통 단일 사용자에게 서비스를 제공하고 FLOPs/byte가 적은 하드웨어를 사용하는 경우에만 해당)과 Transformer 코드베이스 수명 주기의 초기 단계에서의 빠른 반복(단순성 때문에)에만 권장됩니다.

약간 더 나은 접근 방식은 배치 크기 1에서 prefill을 수행하지만(compute-bound이지만 합리적인 지연 시간을 가짐) generation 중에 여러 요청을 함께 배치하는 것입니다:

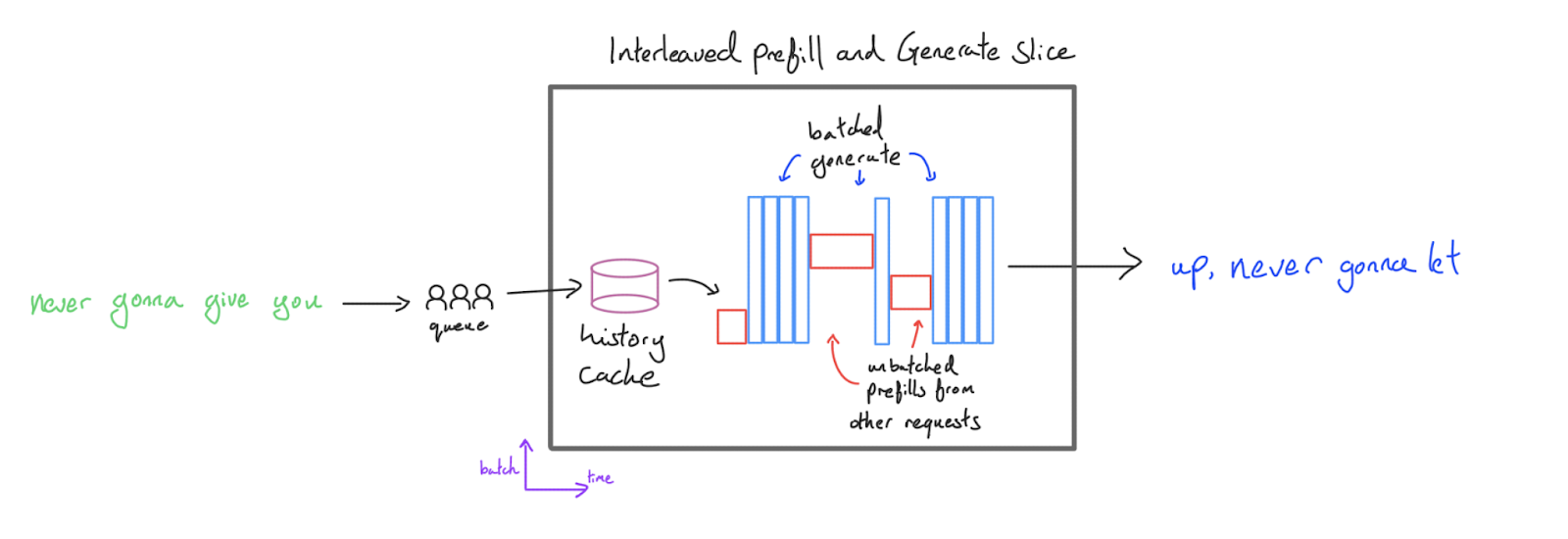
이렇게 하면 generation 처리량을 높게 유지하면서 배치 prefill로 인한 낭비되는 TTFT를 피할 수 있습니다. 이를 인터리브(interleaved) 구성이라고 하는데, prefill과 generation 단계를 “인터리브”하기 때문입니다. 이는 처리량이 주 목표인 평가와 같은 대량 생성 애플리케이션에 매우 강력합니다. 오케스트레이터는 생성 슬롯이 열리는 순간 prefill의 우선순위를 지정하도록 구성하여 매우 큰 generation 배치 크기에서도 높은 활용률을 보장할 수 있습니다. 또한 다른 요청과 배치되지 않으므로 prefill을 최대 길이로 패딩하는 것을 피할 수 있습니다.

주요 단점은 서버가 prefill을 수행할 때 모든 컴퓨팅 리소스가 prefill에 소비되므로 다른 모든 요청의 생성이 일시 중지된다는 것입니다. 응답이 디코딩 중인 사용자 A는 prefill이 발생 중인 사용자 B에 의해 차단됩니다. 이는 TTFT가 개선되었음에도 불구하고 토큰 생성이 불안정하고 평균적으로 느리다는 것을 의미하며, 이는 많은 애플리케이션에서 좋은 사용자 경험이 아닙니다. 다른 사용자의 prefill은 요청의 전체 지연 시간의 critical path에 있습니다.

이를 해결하기 위해 디코드와 prefill을 분리합니다. Transformer 추론은 한 서버에서 수행할 수 있지만, 지연 시간 관점에서는 두 세트의 TPU/GPU에서 두 가지 다른 작업을 실행하는 것이 더 나은 경우가 많습니다. Prefill 서버는 네트워크를 통해 generate 서버로 전송되는 KV 캐시를 생성하고, generate 서버는 여러 캐시를 함께 배치하고 각각에 대한 토큰을 생성합니다. 우리는 이를 “분산형(disaggregated)” 서빙이라고 부릅니다.

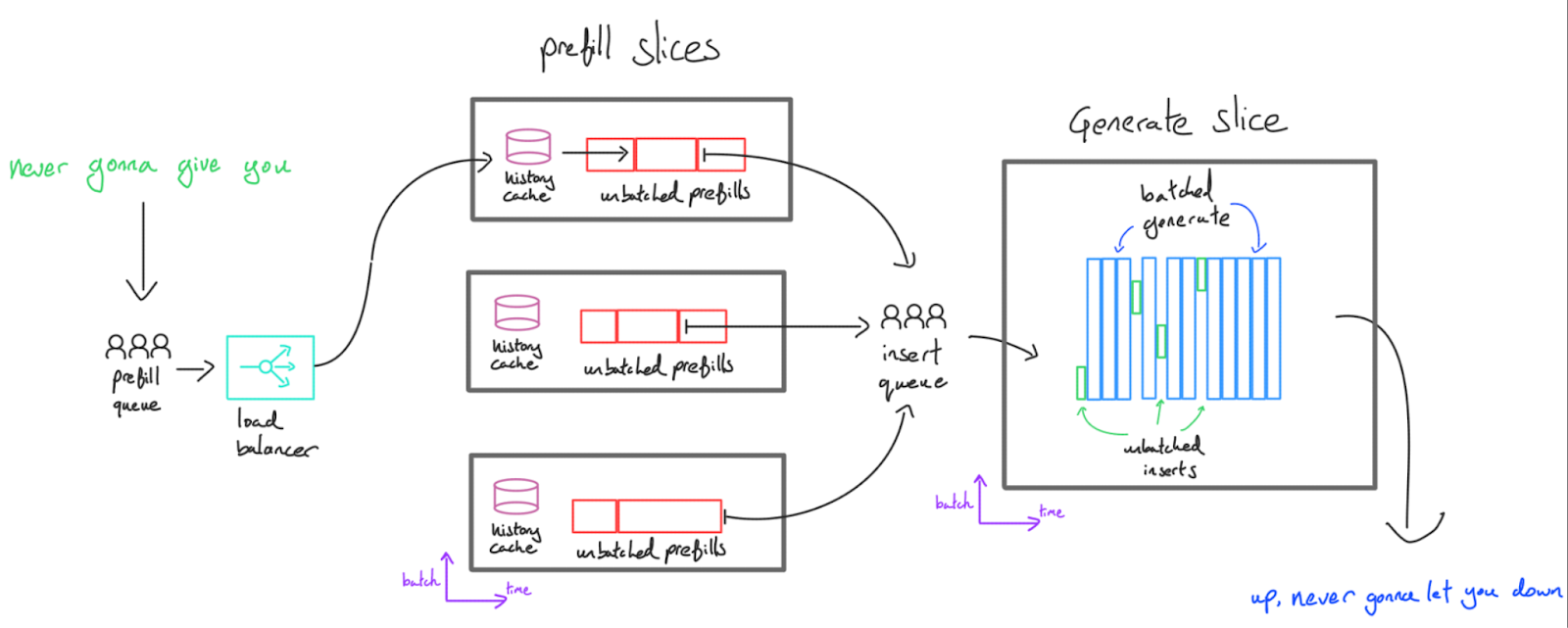
이는 몇 가지 이점을 제공합니다:

  1. 대규모에서의 낮은 지연 시간: prefill 용량이 부족한 경우를 제외하고는 사용자의 요청이 다른 사용자의 요청에 차단되지 않습니다. 요청은 즉시 prefill된 다음 generation 서버로 전송되어 즉시 generation 버퍼에 슬롯되어야 합니다. 많은 동시 요청이 들어올 것으로 예상되는 경우 prefill 서버 수를 generate 서버 수와 독립적으로 확장하여 사용자가 장기간 prefill 대기열에 남지 않도록 할 수 있습니다.

  2. 전문화: 종종 prefill과 generate를 위한 지연 시간 최적 파라미터 샤딩 전략/하드웨어 토폴로지는 상당히 다릅니다(예를 들어, 더 많은 모델 병렬 처리는 generate에는 유용하지만 prefill에는 유용하지 않음). 두 작업이 동일한 샤딩을 사용하도록 제한하면 두 작업의 성능이 저하되고 두 세트의 가중치를 갖는 것은 메모리를 사용합니다. 또한 prefill을 자체 서버로 이동함으로써 현재 처리 중인 것 외에는 KV 캐시를 유지할 필요가 없습니다. 즉, 히스토리 캐싱(다음 섹션 참조)이나 prefill 지연 시간 최적화를 위한 여유 메모리가 훨씬 더 많다는 뜻입니다.

한 가지 단점은 이제 KV 캐시를 네트워크를 통해 이동해야 한다는 것입니다. 이는 일반적으로 허용되지만 KV 캐시 크기를 줄여야 하는 동기를 다시 제공합니다.

Takeaway: 지연 시간에 민감한 고처리량 서빙을 위해 일반적으로 prefill과 generation을 별도의 서버로 분리하며, prefill은 배치 1에서 작동하고 generation은 많은 동시 요청을 함께 배치합니다.

Continuous batching

Continuous batching

위의 문제 (2)는 continuous batching 개념에 동기를 부여합니다. 우리는 다음을 최적화하고 컴파일합니다:

그런 다음 들어오는 요청을 대기열에 넣고, 사용 가능한 generate 슬롯에 따라 prefill 및 generate를 호출하고, 히스토리 캐싱(다음 섹션 참조)을 처리하고, 토큰을 스트리밍하는 오케스트레이터와 이 함수들을 결합합니다.

Prefix caching

Prefix caching

Prefill은 비싸고 compute-bound(여유가 적음)이므로 비용을 줄이는 가장 좋은 방법 중 하나는 덜 하는 것입니다. LLM은 자기회귀적이므로 [“I”, “like”, “dogs”]와 [“I”, “like”, “cats”] 쿼리는 처음 두 토큰에서 동일한 KV 캐시를 생성합니다. 즉, 원칙적으로 “I like dogs” 캐시를 먼저 계산한 다음 “I like cats” 캐시를 계산하면 계산의 1/3만 수행하면 된다는 뜻입니다. 캐시를 재사용하여 대부분의 작업을 절약할 수 있습니다. 이는 몇 가지 특정 경우에 특히 강력합니다:

  1. 챗봇: 대부분의 챗봇 대화는 엄격하게 자신에게 추가되는 주고받는 대화를 포함합니다. 즉, 각 대화 턴에서 KV 캐시를 저장할 수 있다면 최신 토큰을 제외한 모든 토큰에 대한 계산을 건너뛸 수 있습니다.
  2. 퓨샷 프롬프팅: 어떤 종류의 퓨샷 프롬프트라도 있다면, 이를 저장하고 무료로 재사용할 수 있습니다. 시스템 지침도 종종 이 형식을 취합니다.

이것을 수행하기 어려운 유일한 이유는 메모리 제약입니다. 보시다시피 KV 캐시는 크고(종종 수 GB), 캐싱이 유용하려면 후속 쿼리가 도착할 때까지 보관해야 합니다. 일반적으로 prefill 서버의 사용되지 않은 HBM은 로컬 캐싱 시스템에 사용될 수 있습니다. 또한 가속기는 일반적으로 CPU 호스트에 많은 메모리를 가지고 있습니다(예: 8xTPUv5e 서버는 128GiB의 HBM을 가지고 있지만 약 450GiB의 호스트 DRAM을 가짐). 이 메모리는 HBM보다 훨씬 느리지만(보통 생성 단계를 수행하기에는 너무 느림) 캐시 읽기에는 충분히 빠릅니다. 실제로는:

Figure: LRU 트라이로 구현된 KV 접두사 캐시. 접두사를 공유하여 KV 메모리 중복을 피할 수 있습니다. 출처: Character.ai 블로그.

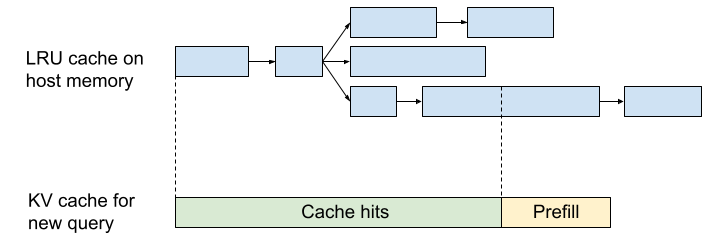
Let’s look at an implementation: JetStream

Google은 JetStream이라는 이 로직을 구현하는 라이브러리를 오픈 소스로 공개했습니다. 서버에는 일반적으로 다른 TPU 슬라이스에 있는 “prefill engines”와 “generate engines” 세트가 있으며 단일 컨트롤러에 의해 조정됩니다. Prefill은 “prefill thread“에서 발생하는 반면 generation은 “generate thread“에서 발생합니다. 또한 prefill에서 generate 슬라이스로 KV 캐시를 복사하는 것을 조정하는 “transfer thread“가 있습니다.

Engine 인터페이스(여기에 구현됨)는 모든 LLM이 제공해야 하는 일반 인터페이스입니다. 주요 메서드는 다음과 같습니다:

JetStream의 PyTorch 버전도 여기에서 사용할 수 있습니다.

Worked Problems

이 섹션을 위해 LLaMA-2 13B를 기반으로 새로운 모델을 만들어 보겠습니다. 세부 사항은 다음과 같습니다:

hyperparam value
L (num_layers) 64
D (d_model) 4,096
F (ffw_dimension) 16,384
N (num_heads) 32
K (num_kv_heads) 8
H (qkv_dim) 256
V (num_embeddings) 32,128

Question 1: 위 모델의 파라미터는 몇 개인가요? int8에서 토큰당 KV 캐시는 얼마나 큰가요? 입력 및 출력 프로젝션 행렬을 공유한다고 가정할 수 있습니다.

답을 보려면 여기를 클릭하세요.

Parameter count: Parameter count:

  • MLP 파라미터 수: $L * D * F * 3$
  • Attention 파라미터 수: $L * 2 * D * H * (N + K)$
  • Vocabulary 파라미터: $D * V$ (이 행렬들을 공유하므로)

따라서 총 파라미터 수는 $L * D * (3F + 2H * (N + K)) + D * V$입니다. 위의 숫자를 대입하면 64 * 4096 * (3*16384 + 2 * 256 * (32 + 8)) + 4096 * 32128 = 18.4e9입니다. 따라서 이 모델은 약 184억 개의 파라미터를 가지고 있습니다.

KV 캐시는 int8에서 토큰당 $2 * L * K * H$이며, 이는 토큰당 2 * 64 * 8 * 256 = 262kB입니다.

Question 2: 이 모델을 TPUv5e 4x4 슬라이스에서 서빙하고 이 토폴로지에 KV 캐시를 완전히 샤딩할 수 있다고 가정해 봅시다. 모든 것에 int8을 사용하고 128k 시퀀스를 지원하고 싶다고 가정할 때 맞출 수 있는 가장 큰 배치 크기는 얼마인가요? KV 헤드 수를 1로 줄이면 어떻게 될까요?

답을 보려면 여기를 클릭하세요.

KV 캐시는 int8에서 토큰당 $2 \cdot L \cdot K \cdot H$, 즉 2 * 64 * 8 * 256 = 262kB 크기를 가집니다. 128k 시퀀스의 경우 배치 항목당 262e3 * 128e3 = 33.5GB를 의미합니다. 각 TPU에는 파라미터를 포함하여 16GB의 HBM이 있으므로, 맞출 수 있는 가장 큰 배치 크기는 (16 * 16e9 - 18.4e9) / 33.5e9 = 7입니다. $K=1$이라면 이것의 8배, 즉 약 56이 될 것입니다.

Question 3: TPU v5e 4x4 슬라이스에서 완전히 샤딩되었다고 가정할 때 HBM에서 MXU로 모든 파라미터를 로드하는 데 얼마나 걸릴까요? int8 파라미터를 가정합니다. 이것은 단계별 지연 시간의 좋은 하한입니다.

답을 보려면 여기를 클릭하세요.

총 18.4B 파라미터, 즉 int8에서 18.4e9 바이트가 있습니다. 칩당 8.1e11 HBM 대역폭이 있으므로, HBM 대역폭을 완전히 사용할 수 있다고 가정하면 대략 18e9 / (8.1e11 * 16) = 1.3ms가 걸릴 것입니다.

Question 4: int8 FLOPs와 파라미터/활성화를 사용하여 TPUv5e 4x4 슬라이스에서 이 모델을 서빙하고 싶다고 가정해 봅시다. prefill과 decode 모두에 대해 어떻게 샤딩하시겠습니까? 힌트: 아마도 다음 질문에 먼저 답해 보세요:

  1. 4x4에서 ICI는 어떻게 보이나요?
  2. 텐서 병렬 처리의 루프라인 경계는 무엇인가요?
  3. KV 캐시를 어떻게 샤딩할 수 있나요?

이 샤딩의 경우, generation에 대한 대략적인 단계별 지연 시간은 얼마인가요?

Question 5: 위의 모델이 실제로 MoE라고 가정해 봅시다. MoE 모델은 사실상 FFW 블록의 E개 사본이 있는 밀집 모델입니다. 각 토큰은 k개의 FFW 블록을 통과하며 이 k개가 평균화되어 출력을 생성합니다. 위 설정에서 E=16 및 k=2를 사용합시다.

  1. 총 파라미터 수와 활성화된 파라미터 수는 몇 개인가요? 활성화되었다는 것은 주어진 토큰에 사용됨을 의미합니다.
  2. TPU v5e에서 FLOPs bound가 되기 위해 필요한 배치 크기는 얼마인가요?
  3. 토큰당 KV 캐시는 얼마나 큰가요?
  4. T 토큰이 있는 순방향 패스에는 얼마나 많은 FLOPs가 포함되나요?
답을 보려면 여기를 클릭하세요.

(1) MoE로서 각 MLP 블록은 이제 밀집 변형보다 $E$ 증가한 $3 * E * D * F$ 파라미터를 가집니다. 따라서 이제 $L * D * (3EF + 2H * (N + K)) + D * V$ 또는 64 * 4096 * (3*16*16384 + 2 * 256 * (32 + 8)) + 4096 * 32128 = 212e9 총 파라미터를 가지며, 이는 약 12배 증가한 것입니다. 활성화된 파라미터의 경우 $E$ 대신 $k$개의 활성화된 파라미터를 가지며 총 64 * 4096 * (3*2*16384 + 2 * 256 * (32 + 8)) + 4096 * 32128 = 31.2e9로, 밀집 변형보다 2배 미만 증가합니다.

(2) $k$배 더 많은 FLOPs에 대해 $E$배 더 많은 파라미터를 가지고 있으므로, HBM 루프라인은 $E/k$배만큼 증가합니다. 이는 TPU v5e에서 약 240 * (16 / 2) = 1920 토큰이 필요함을 의미합니다.

(3) MoE 특성은 어텐션 메커니즘에 대해 아무것도 변경하지 않으므로 KV 캐시 크기는 동일하게 유지됩니다.

(4) 이것은 여전히 $2ND$이며 여기서 $D$는 활성화된 파라미터 수입니다. 따라서 이는 $2 * \text{31.2e9} * T$입니다.

Question 6: MoE를 사용하면 메시의 한 축에 걸쳐 전문가를 분할하는 “expert sharding”을 수행할 수 있습니다. 표준 표기법에서 첫 번째 FFW 가중치는 [E, D, F] 모양을 가지며 [EZ, DX, FY]로 샤딩합니다. 여기서 X는 훈련 중 FSDP 차원으로만 사용됩니다. TPU v5e에서 추론을 수행하고 싶다고 가정해 봅시다:

  1. Y=8, Z=16인 TPU v5e 8x16 슬라이스에서 위 모델에 대한 HBM 가중치 로딩 시간은 얼마인가요? TPU당 사용 가능한 여유 HBM은 얼마인가요?
  2. 우리 모델을 맞출 수 있는 가장 작은 슬라이스는 무엇인가요?

Question 7 [2D model sharding]: 여기서는 ESTI 논문에서 2D weight-stationary sharding이라고 부르는 것의 수학을 다룰 것입니다. 부록 B에서 이에 대해 간단히 설명하지만, 수학을 풀 수 있는지 확인하기 위해 먼저 이 문제를 풀어보세요. 2D weight stationary sharding의 기본 아이디어는 각 청크가 대략 정사각형이 되도록 $D$ 및 $F$ 축 모두를 따라 가중치를 샤딩하는 것입니다. 이는 통신 부하를 줄이고 약간 더 멀리 확장할 수 있게 해줍니다.

다음은 2D weight stationary에 대한 알고리즘입니다:

  1. In[B, DX] = AllGatherYZ(In[B, DXYZ])
  2. Tmp[B, FYZ] {U.X} = In[B, DX] *D Win[DX, FYZ]
  3. Tmp[B, FYZ] = AllReduceX(Tmp[B, FYZ] {U.X})
  4. Out[B, DX] {U.YZ} = Tmp[B, FYZ] *F W2[FYZ, DX]
  5. Out[B, DXYZ] = ReduceScatterYZ(Out[B, DX] {U.YZ})

목표는 이 알고리즘에 대한 $T_\text{math}$와 $T_\text{comms}$를 파악하고 언제 이것이 전통적인 3D 모델 샤딩보다 성능이 뛰어날지 찾는 것입니다.

정답을 보려면 여기를 클릭하세요!

$T_\text{math}$와 $T_\text{comms}$를 계산해 봅시다. 모든 FLOPs는 완전히 샤딩되므로 이전과 같이 $T_\text{math} = 4BDF / (N \cdot C)$이지만 통신은 다음과 같습니다.

\[\begin{align*} T_\text{2D comms} = \frac{2BD}{2X \cdot W_\text{ici}} + \frac{4BF}{YZ \cdot W_\text{ici}} + \frac{2BD}{2X \cdot W_\text{ici}} = \frac{2BD}{X \cdot W_\text{ici}} + \frac{4BF}{YZ \cdot W_\text{ici}} \end{align*}\]

여기서 AllReduce는 두 배 비싸고 각 작업이 수행되는 축 수에 따라 통신을 조정합니다. 토폴로지를 자유롭게 선택할 수 있고 $F=4D$라고 가정하면(LLaMA-2에서와 같이), (기본 미적분학에 의해) $X$, $Y$, $Z$에 대한 최적 값은 $X = \sqrt{N / 8}$, $YZ = \sqrt{8N}$이므로 총 통신은 다음과 같습니다.

\[T_\text{2D comms} = \frac{2B}{W_\text{ici}} \left(\frac{D}{X} + \frac{8D}{YZ}\right) = \frac{\sqrt{128} BD}{\sqrt{N} \cdot W_\text{ici}} \approx \frac{11.3 BD}{\sqrt{N} \cdot W_\text{ici}}\]

첫째, 위에서 복사하면 일반 1D 모델 병렬 처리는 $T_\text{model parallel comms} = 4BD / (3 \cdot W_\text{ici})$를 가지므로, 언제 새로운 통신이 더 작을까요?

\[\begin{align*} T_\text{model parallel comms} > T_\text{2D comms} \iff \frac{4BD}{3 \cdot W_\text{ici}} > \frac{\sqrt{128} BD}{\sqrt{N} \cdot W_\text{ici}} \\ \iff N > 128 \cdot \left(\frac{3}{4}\right)^2 = 81 \end{align*}\]

일반적인 $F$에 대해, 이 조건은 다음과 같다고 주장합니다.

\[N > 32 \cdot \left(\frac{F}{D}\right) \cdot \left(\frac{3}{4}\right)^2\]

따라서 81개 이상의 칩이 있다면 이 새로운 방식을 사용하는 것이 더 낫습니다. 이제 이것은 약간 이상한 결과입니다. 왜냐하면 역사적으로 우리는 약 ~20방향 텐서 병렬 처리에서 ICI 병목 현상을 발견했기 때문입니다. 하지만 여기서 통신 병목 상태일지라도 총 통신은 총 칩 수에 따라 계속 감소합니다! 이것이 말해주는 것은 칩을 늘리고, 배치 크기를 늘리고, 더 많은 파라미터 확장을 수행하고, 감소된 지연 시간을 볼 수 있다는 것입니다.

파트 7은 여기까지입니다! 파트 8(TPU에서 LLaMA 3를 서빙하는 방법에 대한 내용)을 보려면, 여기를 클릭하세요.

Appendix

Appendix A: How real is the batch size > 240 rule?

위에서 제공한 간단한 규칙, 즉 compute-bound가 되려면 배치 크기가 240 토큰보다 커야 한다는 것은 대략적으로 사실이지만, 기기 간 통신을 수행할 때처럼 다른 작업이 사용 가능한 모든 HBM을 사용하지 않는 동안 가중치를 미리 가져오는(prefetch) TPU의 능력을 무시합니다.

다음은 dmodel 8192, dff 32768, 레이어당 2개의 matmul만 있는 소규모 Transformer에 대한 레이어 시간(마이크로초)의 실증적 플롯입니다. 이것은 이 Colab 노트북에서 가져왔습니다. 배치 240 정도까지 단계 시간이 매우 천천히 증가하다가 선형적으로 증가하는 것을 볼 수 있습니다.

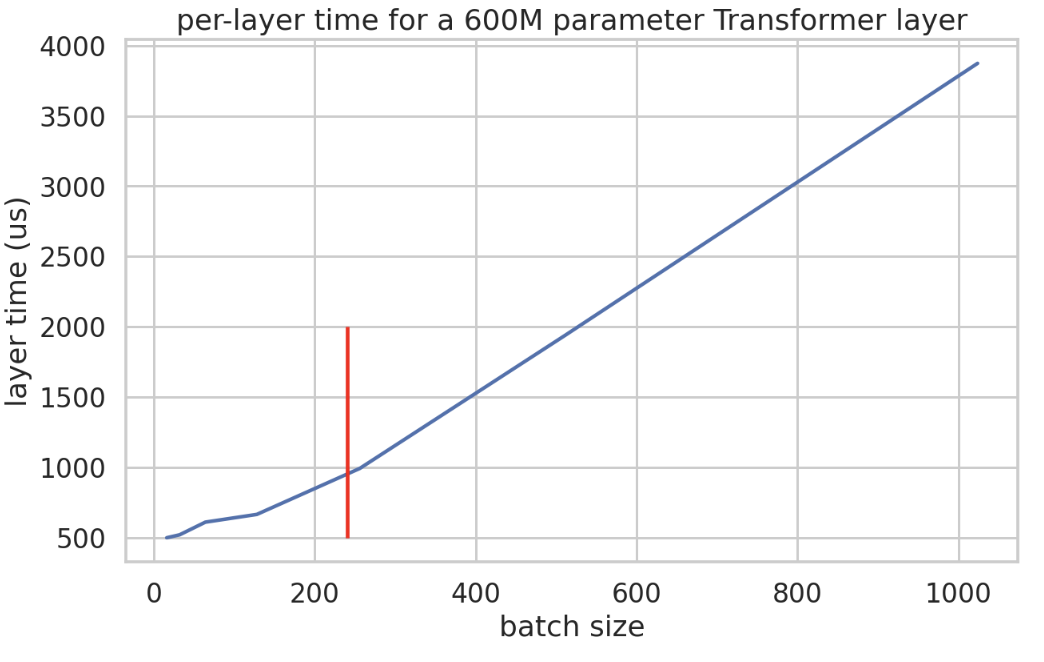
다음은 tokens / us 단위의 실제 처리량입니다. 이것은 주장을 꽤 명확하게 합니다. 우리 레이어는 여기서 4방향으로 샤딩된 약 600M 파라미터이므로 최소 365us 정도의 지연 시간을 예상합니다.

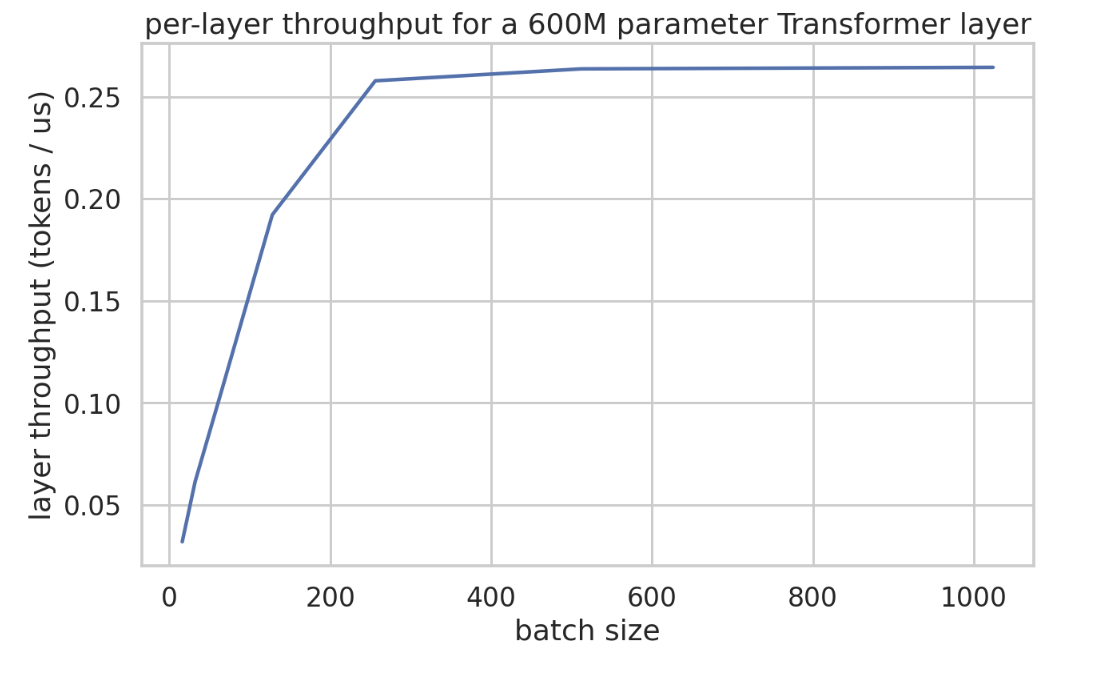
따라서 적어도 이 모델에서는 데이터 병렬 샤드당 약 BS240까지 처리량이 증가하는 것을 실제로 볼 수 있습니다.

Appendix B: 2D Weight Stationary sharding

토폴로지가 커짐에 따라 (TPU와 같은) 고차원 메시에 액세스할 수 있는 경우 “2D Weight Sharding”으로 이를 더욱 개선할 수 있습니다. 두 번째 샤딩 축을 도입함으로써. 우리는 이것을 “2D Weight Stationary“라고 부르며 Efficiently Scaling Transformer Inference 논문에서 더 자세히 설명했습니다.

Megatron에서 히든 \(F\)차원만 샤딩하고 있기 때문에, 1D 샤딩으로 칩 수가 커지면\(E\) (\(d_\text{model}\) 차원)보다 훨씬 작아질 수 있습니다. 이는 더 큰 배치 크기에서 MLP의 첫 번째 레이어가 적용된 후 히든 차원에 대한 집합 연산의 일부를 수행하는 것이 더 경제적일 수 있음을 의미합니다.

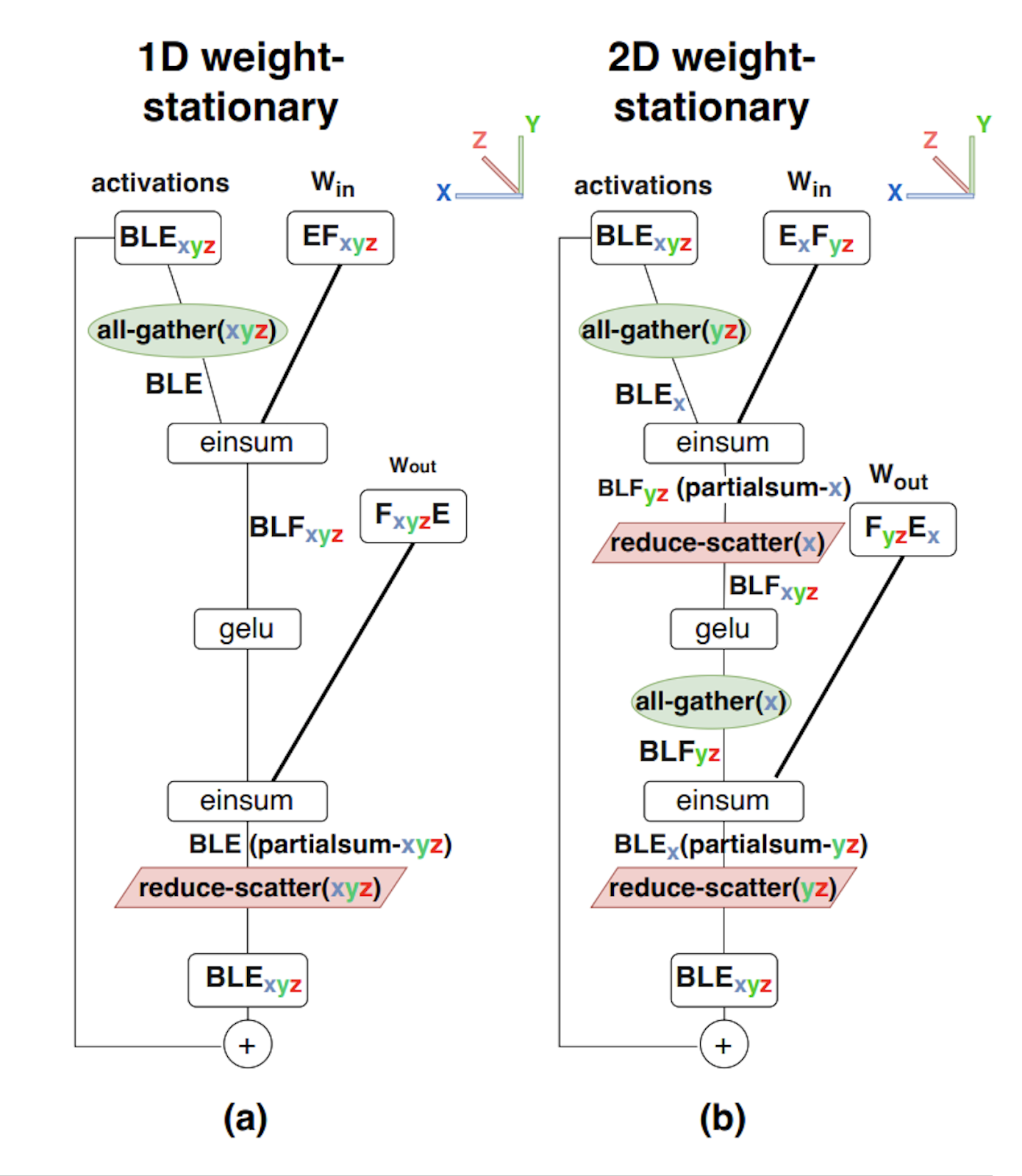
이 그림은 다음을 보여줍니다:

  1. 1D weight-stationary sharding, 일명 순수 Megatron sharding. 여기서 활성화는 AllGather 후 완전히 복제되고 가중치는 히든 F 차원에 대해 완전히 샤딩됩니다.
  2. 2D weight stationary sharding. 여기서 가중치는 히든 F 및 축소 E 차원 모두에 대해 샤딩되고 활성화는 E 차원에 대해 샤딩됩니다. 첫 번째 레이어 전에 (yz) 축에서 AllGather를 수행한 다음 (x) 축에서 ReduceScatter를 수행합니다.

어텐션 레이어의 경우 Megatron 스타일 샤딩도 적은 수의 칩에 대해 비교적 간단합니다. 그러나 Megatron은 \(n_\text{heads}\)차원에 대해 발생하므로 가능한 샤딩 양에 제한을 둡니다. (히든을 샤딩하는 대신\(n_\text{heads}\) 차원을 샤딩하여) 2D 샤딩을 수정하면 더 확장할 수 있는 능력을 얻습니다.

Appendix C: Latency bound communications

요약하자면, 섹션 3에서 우리는 WICI의 전이중 대역폭과 지연 시간 Tmin의 1D 링 링크에서 X 칩에 걸쳐 각 TPU의 크기 B 텐서로 AllGather를 수행하는 데 걸리는 시간을 도출했습니다.

\[T_{total} = \max\left(\frac{T_{min} \cdot |X|}{2}, \frac{B}{W_{ICI}}\right)\]

큰 B의 경우, 시스템에 칩을 더 추가함에 따라 작업을 수행하는 데 필요한 데이터 이동량과 총 사용 가능한 대역폭을 동시에 확장하기 때문에 wall clock은 비교적 일정하게 유지됩니다.

지연 시간 최적화 추론 중에 이동되는 데이터 양이 상대적으로 적기 때문에, 활성화에 대한 집합 연산은 종종 지연 시간 항에 의해 제한됩니다(특히 작은 배치 크기의 경우). 완료되기 전에 완료해야 하는 홉 수를 세어 지연 시간을 아주 쉽게 시각화할 수 있습니다.

TPU에서 통신의 텐서 크기 종속 부분이 홉당 1마이크로초 미만인 경우(홉은 두 인접 디바이스 간의 통신) 집합 연산을 실제로 디스패치하는 고정 오버헤드에 의해 병목 현상이 발생할 수 있습니다. 4.5e10 단방향 ICI 대역폭에서 ICI 통신은 \((\text{bytes} / n_\text{shards}) / 4.5e10 < 1e-6\)일 때 latency bound가 됩니다. 8방향 Megatron 샤딩의 경우 이는 buffer_size < 360kB일 때입니다. 이것은 실제로 추론 중에 그렇게 작지 않습니다: int8에서 BS=16 및 D=8192인 경우 활성화는 16*8192=131kB를 사용하므로 이미 latency bound입니다.

Takeaway: \(\text{total bytes} < W_{ICI} \times 1e-6\)일 때 통신은 latency bound가 됩니다. 예를 들어 \(Y\)에 대한 모델 병렬 처리의 경우, int8에서 \(Y > BD / 45,000\)일 때 bound가 됩니다.

여기서 compute roofline과 비교할 점이 있습니다. 우리는 몇 가지 작은 작업(통신을 위한 지연 시간, matmul을 위한 메모리 대역폭)의 고정 비용을 발생시키고 있습니다.

Appendix D: Speculative Sampling

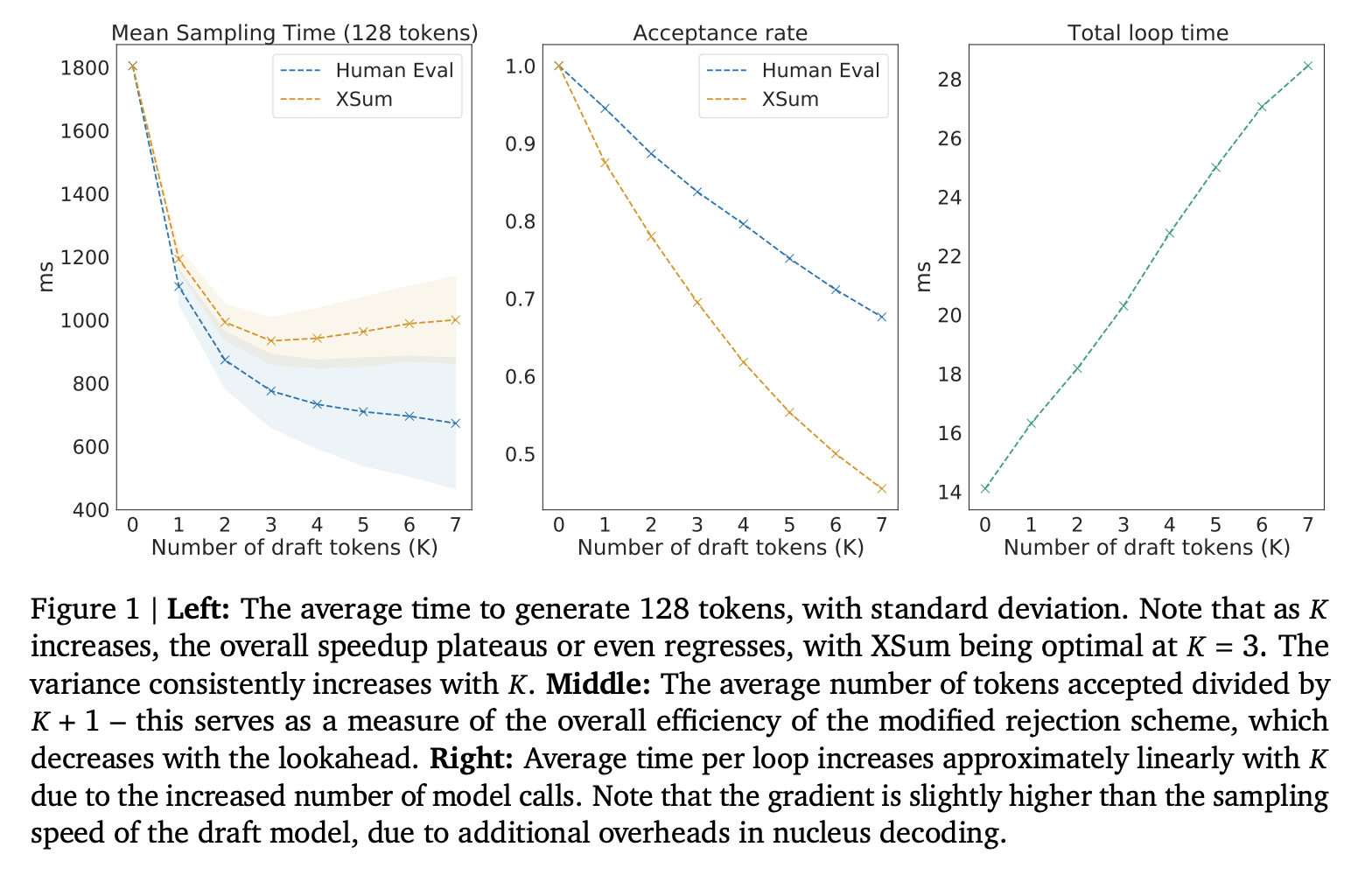
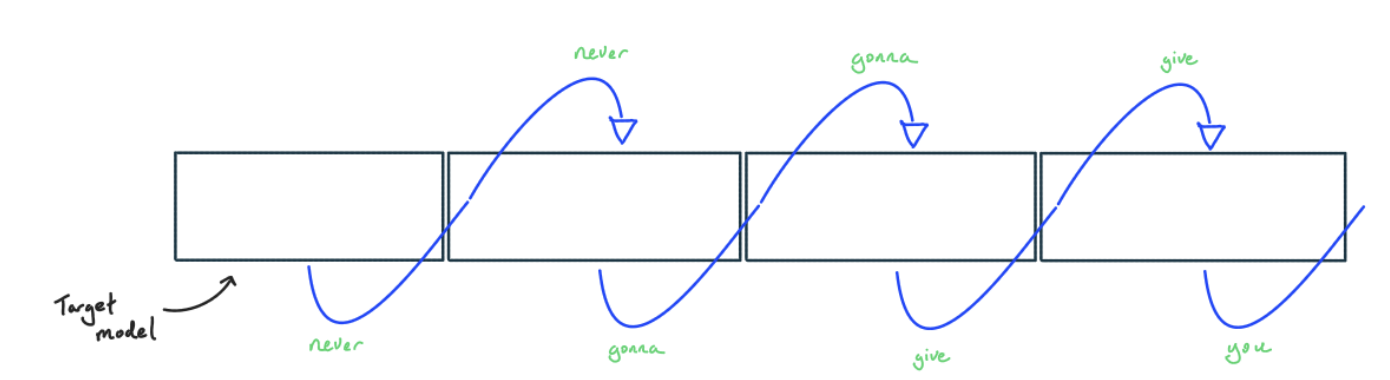
우리가 종단 간 지연 시간에 정말 관심을 가질 때, speculative sampling이라는 추가 트릭을 사용할 수 있습니다. 요약하자면, 우리는 보통 큰 Transformer에서 토큰을 하나씩 생성합니다:

Speculative sampling을 사용하면 더 작고 저렴한 모델을 사용하여 토큰을 생성한 다음 큰 모델로 결과를 확인합니다. 이것은 greedy decoding으로 이해하기 가장 쉽습니다:

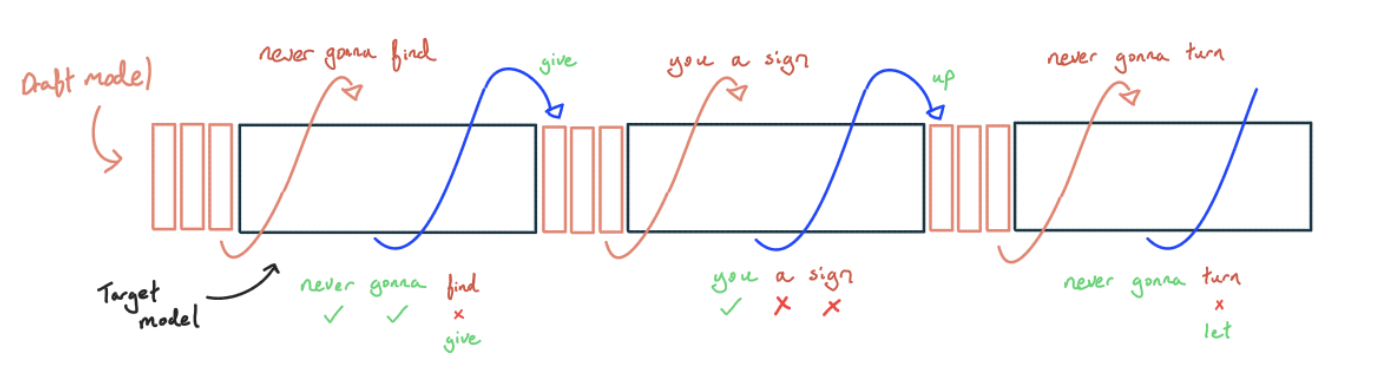
  1. 더 작고 저렴한 모델에서 탐욕스럽게(greedily) 샘플링합니다. 이상적으로는 distillation 등을 통해 더 큰 모델과 일치하도록 훈련된 모델을 사용하지만, 단순히 n-gram을 사용하거나 작은 텍스트 코퍼스를 토큰 매칭하는 것처럼 간단할 수도 있습니다.
  2. K개의 토큰을 생성한 후, 큰 모델을 사용하여 지금까지 생성한 모든 토큰에 대한 다음 토큰 로짓을 계산합니다.
  3. 탐욕스럽게 디코딩하고 있으므로, 작은 모델이 생성한 토큰이 모든 가능한 토큰 중 가장 높은 확률을 갖는지 확인하면 됩니다. 토큰 중 하나가 틀린 경우, 가장 긴 올바른 접두사를 가져와 첫 번째 틀린 토큰을 올바른 토큰으로 바꾼 다음 (1)로 돌아갑니다. 모든 토큰이 맞으면 마지막 올바른 로짓을 사용하여 추가 토큰을 샘플링한 다음 (1)로 돌아갑니다.

왜 이것이 지연 시간 승리일까요? 이 방식은 여전히 모든 토큰에 대해 큰 모델을 통과하는 한 번의 순방향 패스와 동등한 FLOPs를 수행해야 합니다. 하지만 많은 토큰을 함께 배치할 수 있기 때문에 한 번의 순방향 패스에서 이 모든 FLOPs를 수행할 수 있으며, compute-bound가 아니라는 사실을 활용하여 더 많은 토큰을 무료로 얻을 수 있습니다.

수락된 모든 토큰은 평균적으로 FLOPs 측면에서 더 비싸지지만(일부는 거부되고 초안 모델을 호출해야 하므로), 하드웨어에서 더 많은 FLOPs를 짜내고 작은 모델이 저렴하기 때문에 전체적으로 승리합니다. 또한 여러 단계에 걸쳐 KV 캐시 로드를 공유하므로 speculative decoding은 긴 컨텍스트에 대한 처리량 승리가 될 수도 있습니다. 모든 것이 큰 모델에 의해 확인되었으므로 샘플링 분포를 전혀 변경하지 않습니다(단, 비-탐욕적 방식의 경우 정확한 궤적은 다를 수 있음).

전통적으로 speculative decoding은 대상 모델과 유사한 샘플링 분포를 가진 더 작은 모델(예: LLaMA-2 70B의 경우 LLaMA-2 2B)의 존재에 의존하지만, 이는 종종 존재하지 않습니다. 이것이 가능하더라도 수락률이 낮으면 더 작은 drafter가 여전히 너무 비쌀 수 있습니다. 대신 기본 모델의 나중 레이어 중 하나에 전용 drafter 헤드를 추가하는 등 메인 모델 내에 drafter를 내장하는 것이 도움이 될 수 있습니다. 이 헤드는 파라미터의 대부분을 메인 모델과 공유하기 때문에 실행 속도가 빠르고 샘플링 분포가 더 밀접하게 일치합니다.

일반적인 자기회귀 샘플링의 경우 token/s는 단계 시간과 동일합니다. 우리는 여전히 여기의 Arithmetic Intensity 섹션에 따른 이론적 최소 단계 시간에 묶여 있습니다(사실 Speculative Sampling 단계 시간은 일반적으로 일반적인 자기회귀 샘플링보다 상당히 느리지만, 단계당 평균 1개 이상의 토큰을 얻기 때문에 훨씬 더 나은 tokens/s를 얻을 수 있습니다).

Figure: 이 그림은 4B 파라미터 drafter(작은 모델)가 있는 Chinchilla(DeepMind의 70B 모델)의 단계별 지연 시간 및 speculation 성공률을 보여줍니다. XSum(자연어 데이터셋)의 경우 이상적인 speculation 양은 약 3-4 토큰 앞선 반면, HumanEval(코딩 데이터셋)은 더 예측 가능하며 더 공격적인 speculation에서 이득을 봅니다.

비-탐욕적(non-greedy) 디코딩의 경우 어떻게 작동하나요? 이것은 조금 더 복잡하지만, 본질적으로 로짓에서 파생된 \(P_{\text{draft model}}(\text{chosen token})\)및\(P_{\text{target model}}(\text{chosen token})\)을 갖고 이 확률의 비율이 특정 임계값보다 작은 경우 선택한 토큰을 확률적으로 거부하는 Metropolis-Hastings 영감 알고리즘으로 귀결됩니다.

이 두 논문은 이를 동시에 도출했으며 실제로 어떻게 작동하는지에 대한 좋은 예를 가지고 있습니다.

Takeaway: Speculative sampling은 더 나은 토큰당 지연 시간을 위해 처리량을 교환하는 또 다른 강력한 레버입니다. 그러나 배치 크기가 제한되는 시나리오(예: 작은 하드웨어 설치 공간 또는 큰 KV 캐시)에서는 윈윈이 됩니다.

Miscellaneous

*Work done at Google DeepMind, now at MatX.

Citation

For attribution in academic contexts, please cite this work as:

    Austin et al., "How to Scale Your Model", Google DeepMind, online, 2025.

or as a BibTeX entry:

    @article{scaling-book,
      title = {How to Scale Your Model},
      author = {Austin, Jacob and Douglas, Sholto and Frostig, Roy and Levskaya, Anselm and Chen, Charlie and Vikram, Sharad
      and Lebron, Federico and Choy, Peter and Ramasesh, Vinay and Webson, Albert and Pope, Reiner},
      publisher = {Google DeepMind},
      howpublished = {Online},
      note = {Retrieved from https://jax-ml.github.io/scaling-book/},
      year = {2025}
    }