How to Profile TPU Programs

Part 9 of How To Scale Your Model (Part 8: Serving LLaMA | Part 10: JAX)

지금까지 이 시리즈는 전적으로 이론적이었습니다: 하드웨어 루프라인에 기반한 대략적인 계산들이었죠. 그러한 이해가 여러분을 멀리 데려가 주지만, 많은 최적화는 실질적인 세부 사항으로 귀결됩니다: XLA 컴파일러가 어떻게 작동하는지, 그리고 JAX/Tensorboard Profiler와 같은 프로파일링 도구를 사용하여 예상대로 작동하지 않을 때 무엇을 해야 하는지 파악하는 방법 등이죠. 여기서는 이에 대해 논의합니다.

번역 안내: 원저자(Jacob Austin)의 허락을 받아 원문을 번역 중입니다.
해당 글의 1인칭은 원문 저자를 지칭합니다.
원문: How to Scale Your Model
번역: 신종훈

A Thousand-Foot View of the TPU Software Stack

Google은 고수준 JAX 코드부터 저수준 Pallas나 HLO에 이르기까지 TPU 프로그래밍을 위한 다양한 API를 제공합니다. 대부분의 프로그래머는 JAX 코드를 독점적으로 작성하며, 이를 통해 TPU에서 효율적으로 실행되도록 자동으로 컴파일되는 추상적인 NumPy 스타일의 선형 대수 프로그램을 작성할 수 있습니다.

다음은 두 행렬을 곱하는 간단한 예제 JAX 프로그램입니다:

import jax
import jax.numpy as jnp

def multiply(x, y):
  return jnp.einsum('bf,fd->db', x, y)

y = jax.jit(multiply)(jnp.ones((128, 256)), jnp.ones((256, 16), dtype=jnp.bfloat16))

jax.jit을 호출함으로써 우리는 JAX에게 이 함수를 추적하고 StableHLO라고 하는 더 낮은 수준의 IR(ML 계산을 위한 플랫폼 불가지론적 IR)을 내보내도록 지시합니다. 이는 다시 XLA 컴파일러에 의해 HLO로 낮아집니다(lowered). 컴파일러는 JAX 프로파일에서 관찰할 수 있는 HLO를 생성하기 위해 fusion, 레이아웃 및 기타 요소를 결정하는 많은 패스를 실행합니다. 이 HLO는 JAX 코드의 모든 핵심 선형 대수 연산(matmuls, pointwise ops, convolutions 등)을 LLVM 스타일 그래프 뷰로 나타냅니다. 예를 들어, 위 프로그램의 축약된 HLO 버전은 다음과 같습니다이 HLO를 얻으려면 `jax.jit(f).lower(*args, **kwargs).compile().as_text()`를 실행하면 됩니다.:

ENTRY %main.5 (Arg_0.1: f32[128,256], Arg_1.2: bf16[256,16]) -> f32[16,128] {
  %Arg_1.2 = bf16[256,16]{1,0} parameter(1), metadata={op_name="y"}
  %convert.3 = f32[256,16]{1,0} convert(bf16[256,16]{1,0} %Arg_1.2),
  %Arg_0.1 = f32[128,256]{1,0} parameter(0), metadata={op_name="x"}
  ROOT %dot.4 = f32[16,128]{1,0} dot(f32[256,16]{1,0} %convert.3, f32[128,256]{1,0} %Arg_0.1), lhs_contracting_dims={0}, rhs_contracting_dims={1},
}

잠시 후에 HLO 구문을 설명하겠지만, 지금은 이것이 위의 JAX 코드와 꽤 잘 일치한다는 점만 알아두세요. 예를 들어,

ROOT %dot.4 = f32[16,128]{1,0} dot(f32[256,16]{1,0} %convert.3, f32[128,256]{1,0} %Arg_0.1), lhs_contracting_dims={0}, rhs_contracting_dims={1}

이것은 각각 0과 1 차원을 따라 두 f32 행렬을 곱하는 실제 matmul입니다.

이 HLO를 TPU에서 실행할 수 있는 코드로 변환하기 위해, XLA 컴파일러는 먼저 이를 LLO(low-level optimizer) IR로 낮춥니다. LLO는 TPU를 직접 프로그래밍하여 메모리 간 복사 예약, 시스톨릭 배열로 배열 푸시 등을 수행합니다. LLO 코드에는 시스톨릭 배열로 버퍼를 푸시하고, 결과를 가져오고, TPU 메모리의 다른 부분 간에 통신하는 DMA를 예약하는 기본 요소(primitives)가 포함되어 있습니다. LLO로 낮아지면 TPU IMEM에 로드되어 실행되는 기계어 코드로 컴파일됩니다.

프로그램이 우리가 원하는 것보다 느리게 실행될 때, 우리는 주로 성능을 개선하기 위해 JAX 수준에서 작업합니다. 그러나 그렇게 하려면 종종 HLO의 의미와 코드가 TPU에서 실제로 어떻게 실행되는지 이해해야 합니다. 낮은 수준에서 문제가 발생하면, 우리는 또 다른 탈출구를 찾아 Pallas로 커스텀 커널을 작성합니다. 프로그램의 HLO와 런타임 통계를 보려면 JAX 프로파일러를 사용합니다.

The JAX Profiler: A Multi-Purpose TPU Profiler

JAX는 프로그램이 실행될 때 TPU에서 무슨 일이 일어나고 있는지 이해하기 위한 유용한 도구가 포함된 다목적 TPU 프로파일러를 제공합니다. jax.profiler 모듈을 사용하여 실행 중인 프로그램을 추적하고 각 하위 구성 요소의 지속 시간, 각 프로그램의 HLO, 메모리 사용량 등 모든 것을 기록할 수 있습니다. 예를 들어, 이 코드는 /tmp/tensorboard 파일에 트레이스(trace)를 덤프하며, 이는 TensorBoard에서 볼 수 있습니다 (여기 단계별 가이드가 있습니다).

import jax
with jax.profiler.trace("/tmp/tensorboard"):
  key = jax.random.key(0)
  x = jax.random.normal(key, (1024, 1024))
  y = x @ x
  y.block_until_ready()

# Now you can load TensorBoard in a Google Colab with
#
# !pip install tensorboard tensorboard-plugin-profile
# !pip install tensorboard tensorboard-plugin-profile
# %load_ext tensorboard
# %tensorboard --logdir=/tmp/tensorboard
#
# or externally with
#
# > tensorboard --logdir=/tmp/tensorboard
#

다음은 프로파일러에서 수행할 수 있는 작업에 대한 개요입니다:

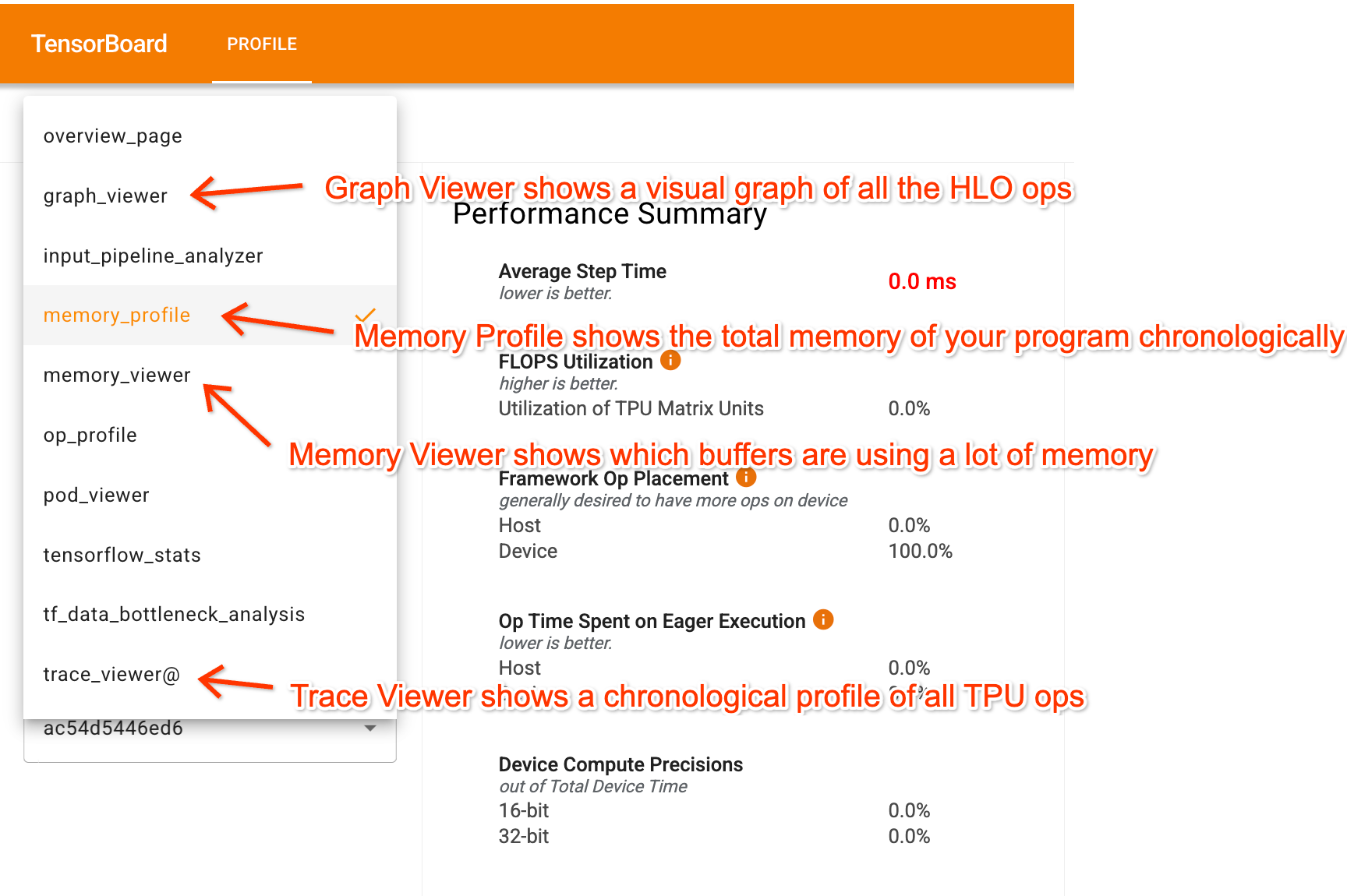
TensorBoard에 들어가면, 프로파일러에는 프로그램을 이해하는 데 도움이 되는 몇 가지 주요 탭이 있습니다:

Trace Viewer는 TPU에서 실제로 무슨 일이 일어나고 있는지 상세한 타임라인으로 보여줍니다.
Graph Viewer는 HLO 그래프를 보여주어, 프로그램의 어떤 부분이 서로 연결되고 어떻게 샤딩되는지 볼 수 있게 해줍니다.
Memory Profile 및 Memory Viewer: 프로그램이 얼마나 많은 메모리를 사용하고 있는지 보여줍니다.

프로파일을 공유하기는 다소 어렵지만, 여기 간단한 Transformer에 대한 Trace Viewer 구성 요소가 포함된 Perfetto 링크가 있습니다. 이 Colab을 통해 전체 JAX/TensorBoard 트레이스를 생성하고 직접 실행해 볼 수 있습니다.

Trace Viewer

Trace Viewer는 아마도 프로파일러에서 가장 유용한 부분일 것입니다. 아래 예시는 주석이 달린 간단한 Transformer를 보여줍니다. 이름은 코드에서 제공된 레이블에서 나옵니다.

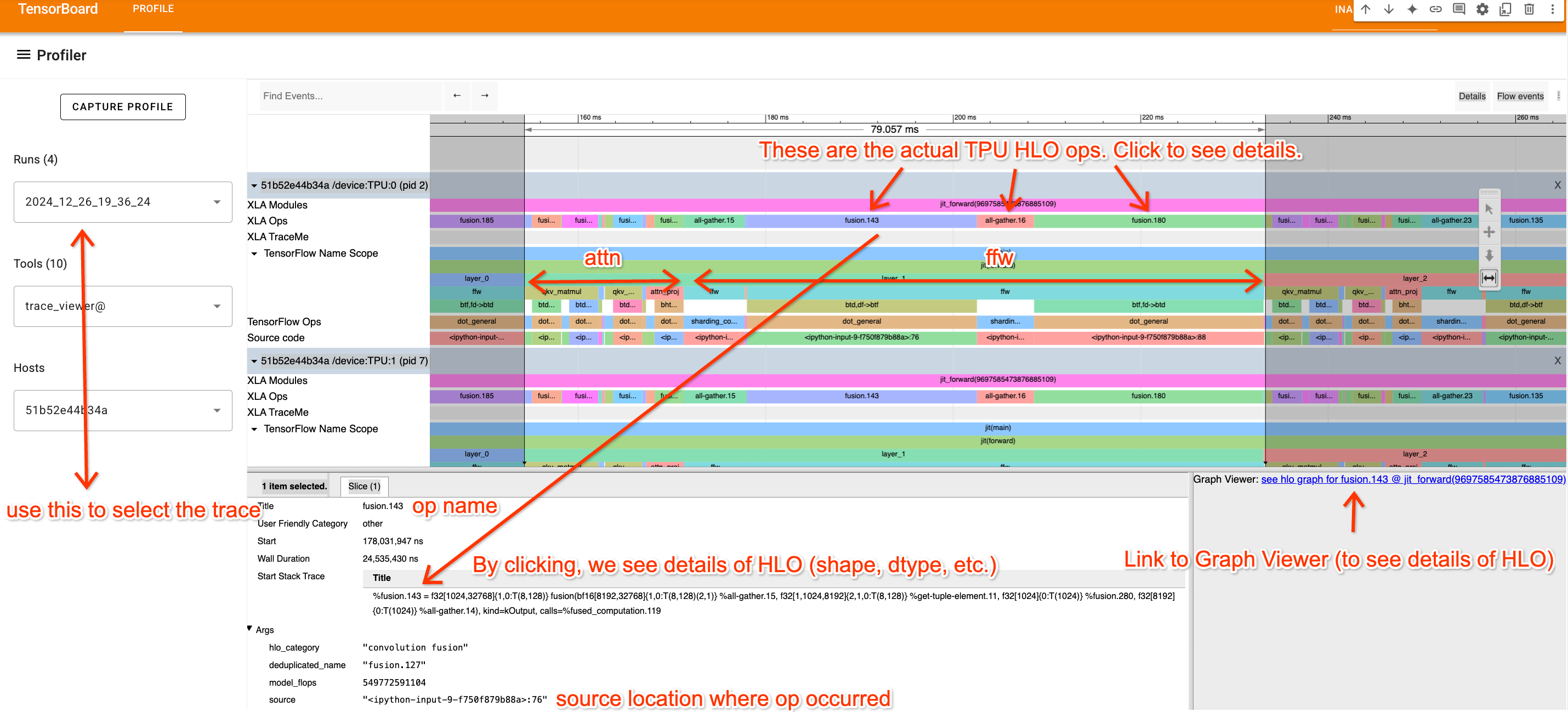
Trace Viewer는 각 TPU 코어의 모든 작업에 대한 시간순 타임라인을 보여줍니다. 일반적으로 모든 TPU가 동일한 명령어를 실행하므로 여기서는 TPU:0만 보고 있습니다. 몇 가지 주요 사항:

맨 윗줄(XLA Ops)은 실제 TPU 연산(이름은 HLO 이름임)을 보여줍니다. 다른 모든 것은 jax.named_scope, jax.named_call 및 Python 스택 트레이스에 기반한 대략적인 트레이스입니다.
반복되는 블록을 통해 여기서 단일 레이어를 격리할 수 있습니다. 또한 (코드를 보거나 Transformer 작동 방식을 이해하여) 어떤 부분이 attention이고 어떤 부분이 MLP인지 알 수 있습니다.
XLA op을 클릭하면 코드가 어디에서 왔는지 확인(트레이스를 이해하는 데 유용)하고 Graph Viewer로 연결되는 링크를 볼 수 있습니다.

Tip: A/D로 좌우로 이동하고 W/S로 확대 및 축소하는 “비디오 게임” 스타일 컨트롤을 사용하여 Trace Viewer를 탐색할 수 있습니다. 이 컨트롤을 사용하면 탐색이 훨씬 쉬워집니다.

How to read an XLA op

HLO는 실제로 읽기 그리 어렵지 않으며, 위의 트레이스에서 특정 부분이 무엇에 해당하는지 이해하는 데 매우 유용합니다. 다음은 fusion.3이라는 예제 op입니다.

%fusion.3 = bf16[32,32,4096]{2,1,0:T(8,128)(2,1)S(1)} fusion(bf16[32,32,8192]{2,1,0:T(8,128)(2,1)S(1)} %fusion.32), kind=kCustom, calls=%all-reduce-scatter.3

이것을 부분별로 분석해 보겠습니다.

Op Name: fusion.3
- dot 또는 fusion op은 최대 1개의 행렬 곱셈과 가능한 여러 관련 pointwise VPU-ops를 포함하는 연산 집합입니다.
Shape/layout: bf16[32,32,4096]
- 이것은 op의 출력 형태입니다. dtype이 bf16(파라미터당 2바이트)이고 [32,32,4096]이 형태임을 알 수 있습니다.
Layout: {2,1,0:T(8,128)(2,1)}
- {2,1,0:T(8,128)(2,1)}은 메모리 내 축의 순서(column major, row major 등)와 배열 패딩을 알려줍니다. 자세한 내용은 아래에 있습니다.
Memory location: S(1)
- S(1)은 이 배열이 VMEM에 있음을 알려줍니다. S(0)(때로는 생략됨)는 HBM입니다. S(2)와 S(3)는 다른 메모리 공간입니다.
Arguments: bf16[32,32,8192]{2,1,0:T(8,128)(2,1)S(1)} %fusion.32
- 이 op은 특정 형태를 가진 fusion.32라는 bf16 배열 하나를 입력으로 가집니다. 이것은 어떤 함수가 이 함수로 들어가는지 알려줍니다.

이 표기법을 좀 더 이해해 봅시다. 간단한 예로 다음을 들어보겠습니다:

f32[3,5]{1,0:T(2,2)}

이것 역시 이 Op이 특정 타일링 {1,0:T(2,2)}을 가진 [3, 5] 형태의 float32 배열을 반환한다고 말합니다. 타일링이 너무 중요하지는 않지만 간단히 말해서, 타일링은 N차원 배열이 메모리에 순차적으로 배치되는 방식을 알려줍니다. 다음은 이 배열이 어떻게 배치되는지 보여주는 다이어그램입니다:

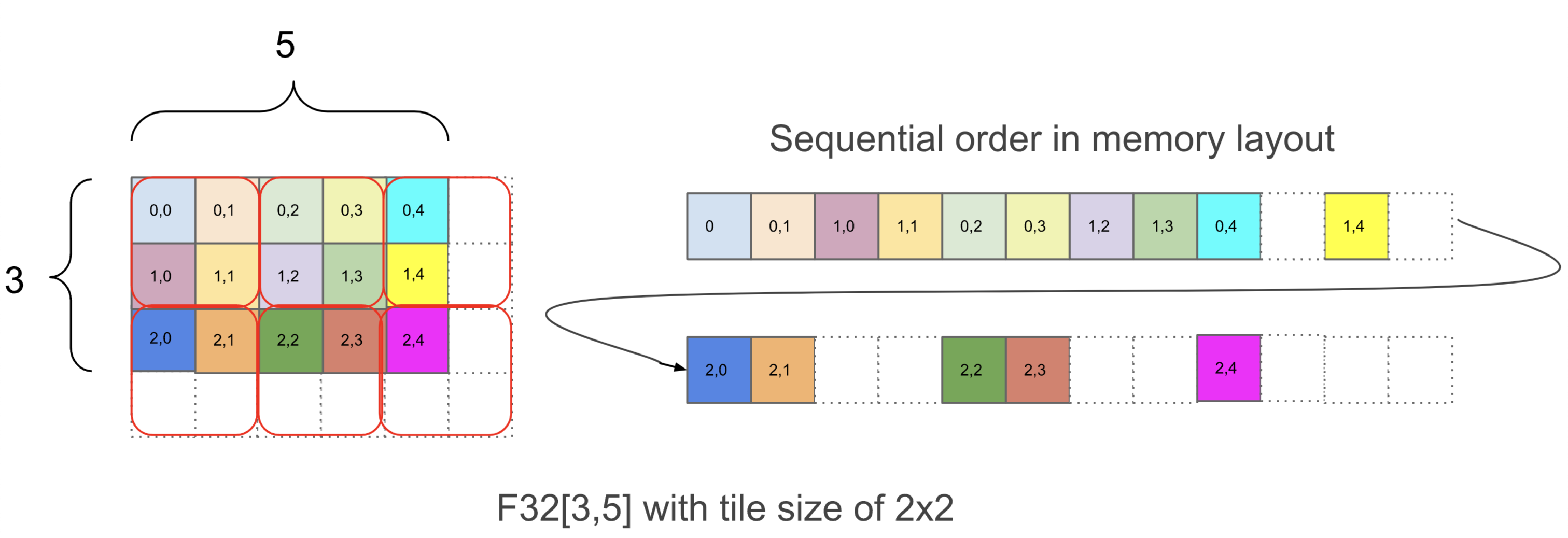
{1,0:T(2,2)} 내에서 1,0 부분은 실제 메모리에서 배열 차원의 순서를 가장 작은(minor) 것부터 가장 큰(major) 것 순서로 알려줍니다. 오른쪽에서 왼쪽으로 읽어서 f32[3,5]의 해당 차원을 선택하여 배열의 물리적 레이아웃을 파악할 수 있습니다. 이 예제에서 물리적 레이아웃은 [3,5]로 논리적 형태와 동일합니다. 그 후 T(2,2)는 배열이 (2, 2) 청크로 타일링됨을 알려줍니다. 각 청크 내에서 배열은 행 우선(row-major)이고, 그 다음 열입니다. 즉 (0, 0) 다음에 (0, 1), 그 다음 (1, 0)과 (1,1)이 옵니다. T(2, 2) 타일링 때문에 배열은 [4, 6]으로 패딩되어 메모리 사용량이 약 1.6배 확장됩니다. 위에서 주어진 큰 bf16 배열 bf16[32,32,8192]{2,1,0:T(8,128)(2,1)S(1)}의 경우, T(8,128)(2,1)을 수행합니다. 이는 배열에 두 단계의 타일링, 즉 외부 (8, 128) 타일링과 그 유닛 내부의 내부 (2, 1) 타일링(bf16 로드가 항상 4바이트의 배수가 되도록 사용됨)이 있음을 알려줍니다. 예를 들어, bf16[4,8]{1,0,T(2,4)(2,1)}는 다음과 같습니다 (색상은 (2,4) 타일, 빨간 상자는 (2,1) 타일):

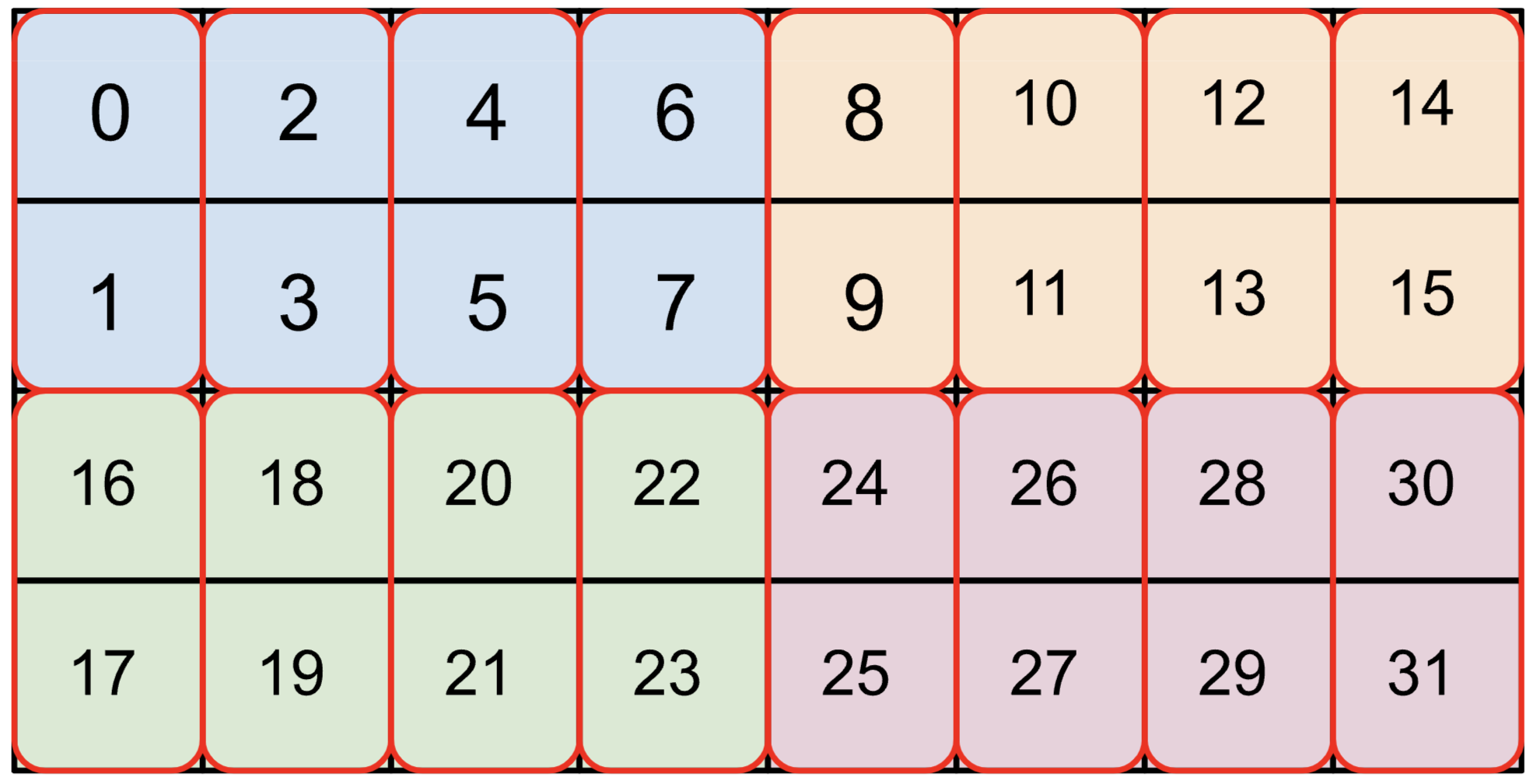
타일링은 텐서 청크를 VMEM에 얼마나 효율적으로 로드할 수 있는지에 영향을 줄 수 있으며, XLA는 때때로 프로그램 내에서 텐서를 “retile”하거나 “re-layout”하는 복사본을 도입하는데, 때로는 상당한 오버헤드가 발생합니다.JAX는 XLA가 프로그램 입력에 대해 "선호하는" 레이아웃을 계산할 수 있도록 하여 이 문제를 해결하는 실험적 기능을 제공합니다. `jax.jit`으로 프로그램을 "just-in-time" 컴파일할 때 일반적으로 JAX에 어떤 형태와 dtype을 예상하는지 알려주는 "mock" 입력을 전달합니다. 여기에는 일반적으로 최적이 아닐 수 있는 타일링 정보도 포함됩니다. 대신 입력 레이아웃을 AUTO로 지정하면 `jax.jit`은 jitted 프로그램이 선호하는 레이아웃을 반환합니다. 그런 다음 텐서를 해당 레이아웃으로 명시적으로 로드하여 프로그램 내에서 복사를 유발하는 것을 피할 수 있습니다.

Graph Viewer

위의 일부 fusion은 복잡해 보일 수 있지만, XLA Graph Viewer를 사용하면 파싱하기가 더 쉽습니다. 예를 들어, 다음은 꽤 복잡한 fusion의 모습입니다:

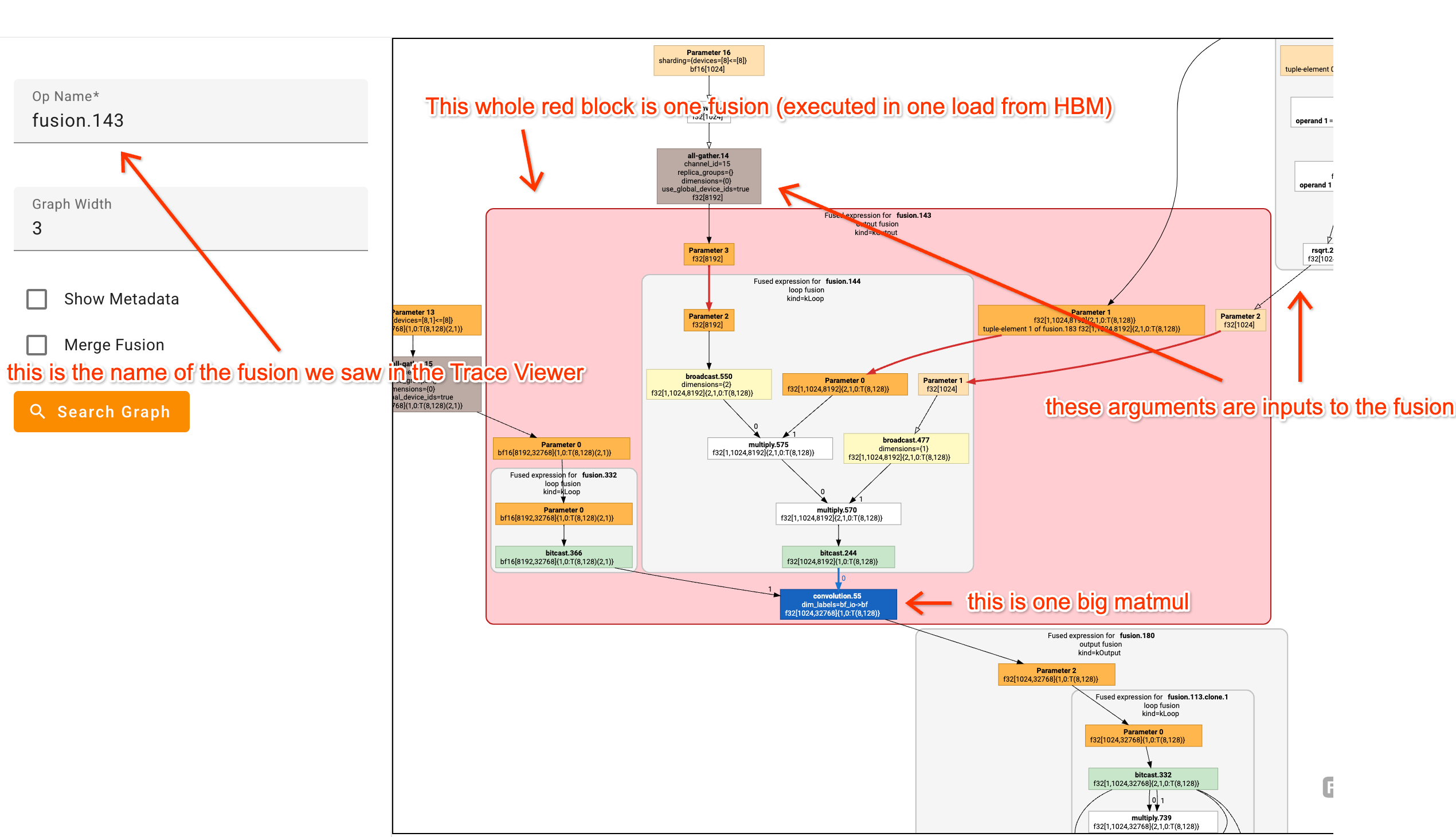
많은 HLO 그래프를 쳐다보며 HLO op을 프로파일링 중인 코드에 매핑하려고 시도하는 것은 정말 도움이 됩니다. 상자 위에 마우스를 올리면 함수가 정의된 코드 줄이 표시되는 경우가 많습니다.

Looking at a real(ish) example profile

이 Colab에는 가짜 Transformer에 대한 예제 프로파일이 있습니다. 급한 경우 Trace Viewer를 볼 수 있는 Perfetto 링크가 여기에 있습니다. 무슨 일이 일어나고 있는지 식별할 수 있도록 평소보다 더 많은 노력을 들여 jax.named_scope 호출로 트레이스에 주석을 달았습니다.

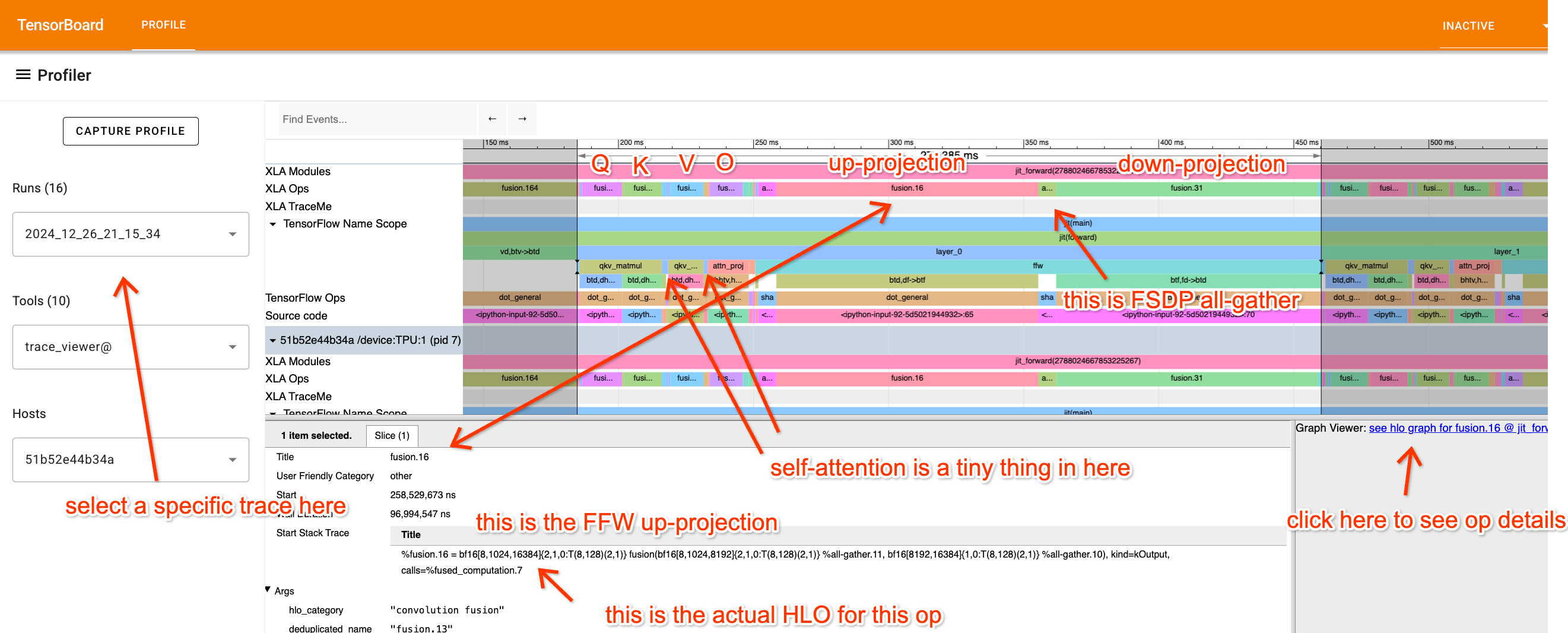
프로파일을 살펴보고 각 부분이 무엇을 하고 있는지 정말 이해하려고 노력해 보세요. FFW 블록부터 시작해서 조금씩 분석해 봅시다:

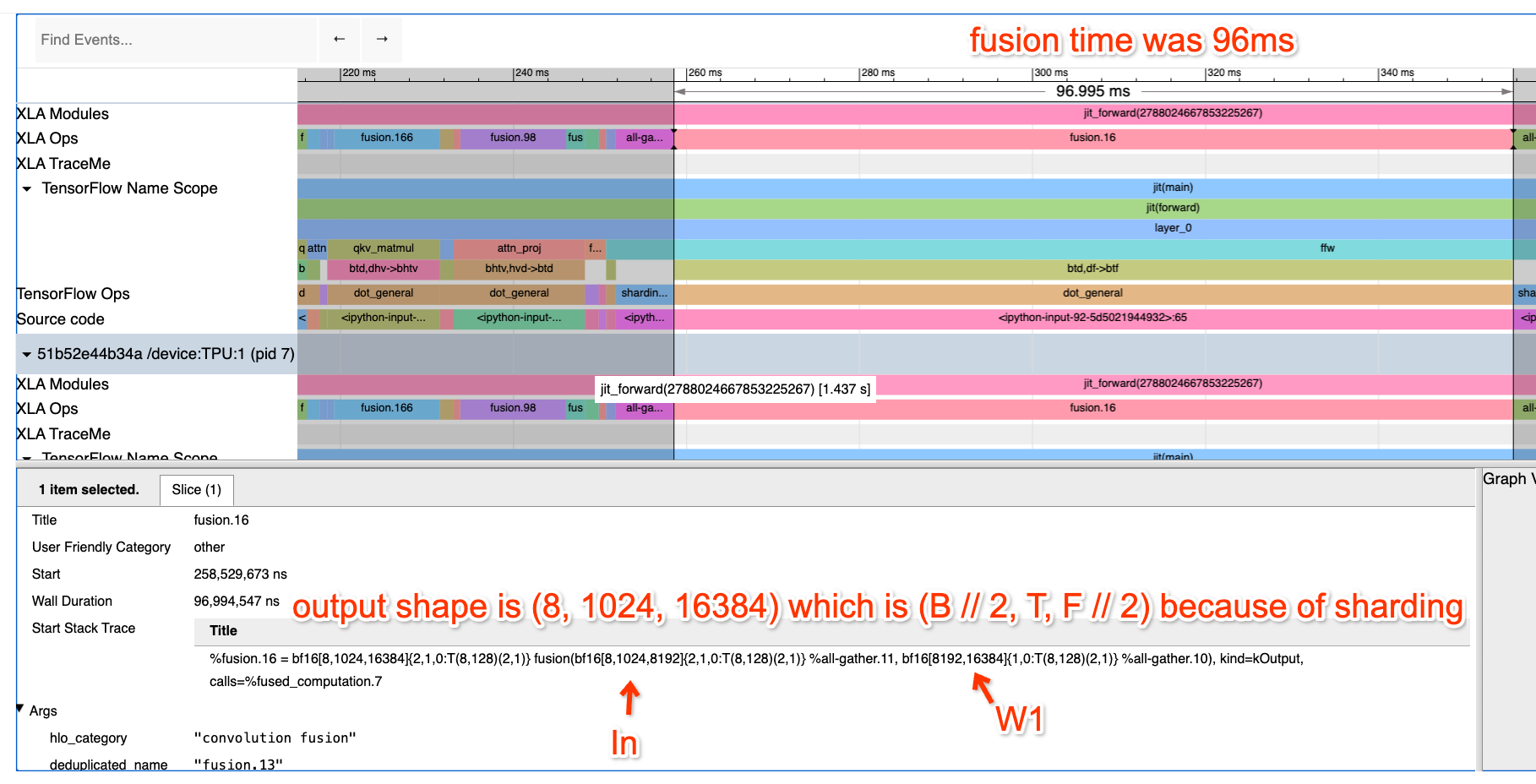
여기서는 FFW 블록을 확대했습니다. up-projection Op이 입력 bf16[8, 1024, 8192] 및 bf16[8192, 16384]와 출력 bf16[32, 1024, 16384]를 가진 fusion(matmul)임을 알 수 있습니다. 저는 (이 코드를 작성했기 때문에) 이것이 4방향 DP, 2방향 MP 샤딩된 matmul의 로컬 뷰라는 것을 알고 있으므로 실제로는 다음을 수행하고 있습니다.

X: bf16[32, 1024, 8192] * W_in: bf16[8192, 32768] -> Tmp: bf16[32, 1024, 32768]

이 작업에 얼마나 걸릴 것으로 예상합니까? 우선 데이터 병렬 샤드당 배치 크기는 8 * 1024 = 8192이므로 확실히 compute-bound여야 합니다. 이것은 8개의 TPUv2 코어(Google Colab에서 무료로 사용 가능)에 있으므로 약 2 * 32 * 1024 * 8192 * 32768 / (23e12 * 8) = 95.6ms가 걸릴 것으로 예상하며, 이는 실제 걸리는 시간(96ms)과 거의 정확히 일치합니다. 훌륭합니다! 이는 우리가 환상적인 FLOPs 활용률을 얻고 있음을 의미합니다!

통신은 어떤가요? 두 번째 matmul 끝에 숨겨진 작은 fusion을 볼 수 있습니다. 클릭하면 다음을 볼 수 있습니다.

%fusion.1 = bf16[8,1024,4096]{2,1,0:T(8,128)(2,1)} fusion(bf16[8,1024,8192]{2,1,0:T(8,128)(2,1)} %fusion.31), kind=kCustom, calls=%all-reduce-scatter.1

이것은 기본적으로 작은 ReduceScatter입니다(여기 GraphViewer가 있습니다);

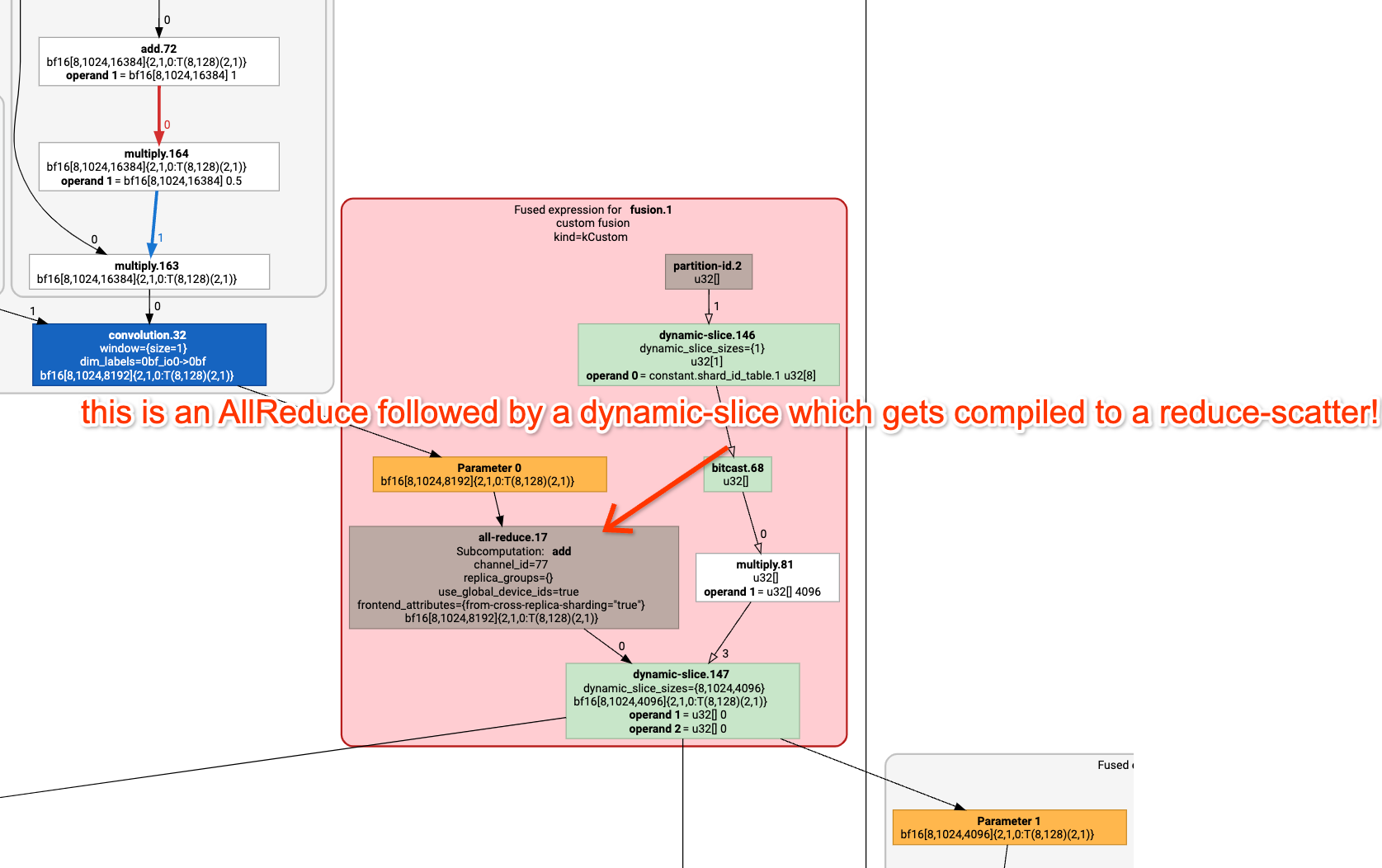
이 작업에 얼마나 걸릴 것으로 예상합니까? 글쎄요, TPUv2 4x2에서 ReduceScatter를 수행하고 있으므로 1.2e11 양방향 대역폭에서 한 번의 홉만 필요합니다. 배열 크기는 2*32*1024*8192이며 배치 축이 4방향으로 샤딩되므로 각 샤드는 2*8*1024*8192=134MB입니다. 따라서 대략 1.1ms가 걸릴 것입니다. 실제로는 얼마나 걸릴까요? 프로파일에 1.13ms로 보고되었습니다. 따라서 우리는 루프라인에 정말 가깝습니다!

Attention도 살펴봅시다! 다음은 attention 구성 요소의 프로파일입니다:

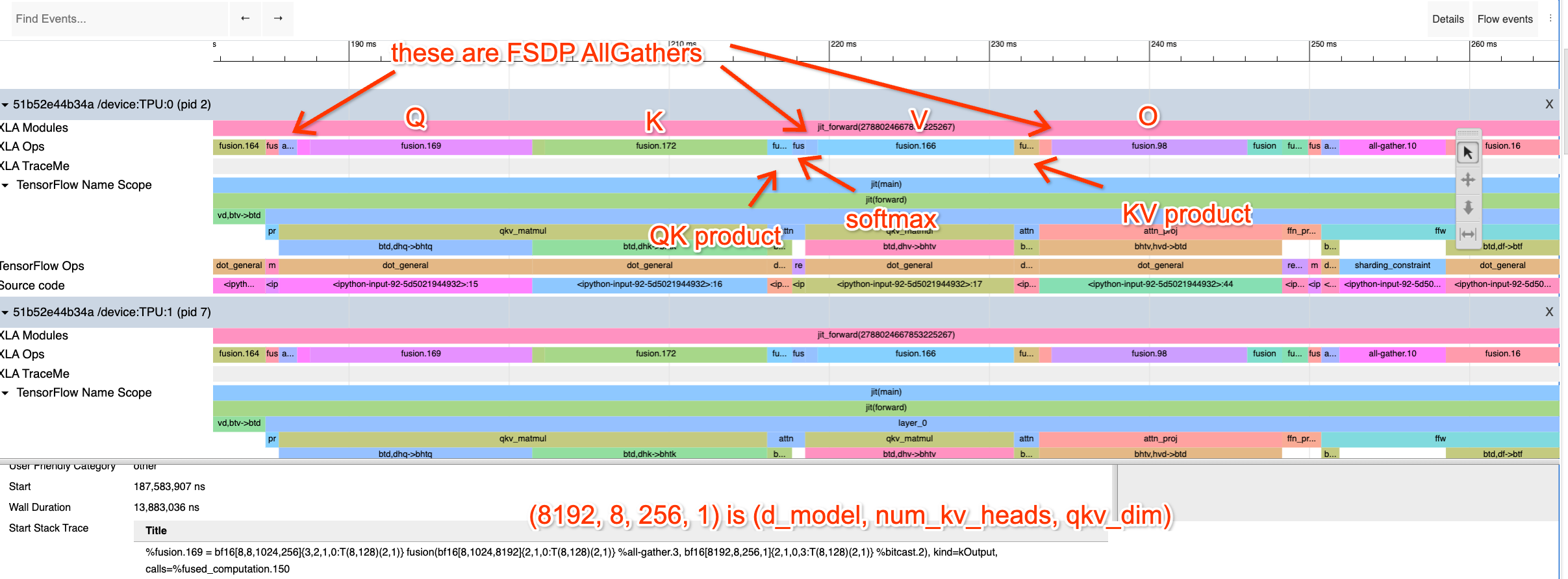
Q 프로젝션 op을 클릭했는데, 이는 [d_model = 8192, n_heads = 32, d_qkv = 256] 모양의 행렬 \(W_Q\)를 사용합니다. 헤드 차원을 따라 Megatron 샤딩하고 있습니다. 이것들이 얼마나 걸릴지 계산하는 동일한 연습을 해보세요.

Memory Profile

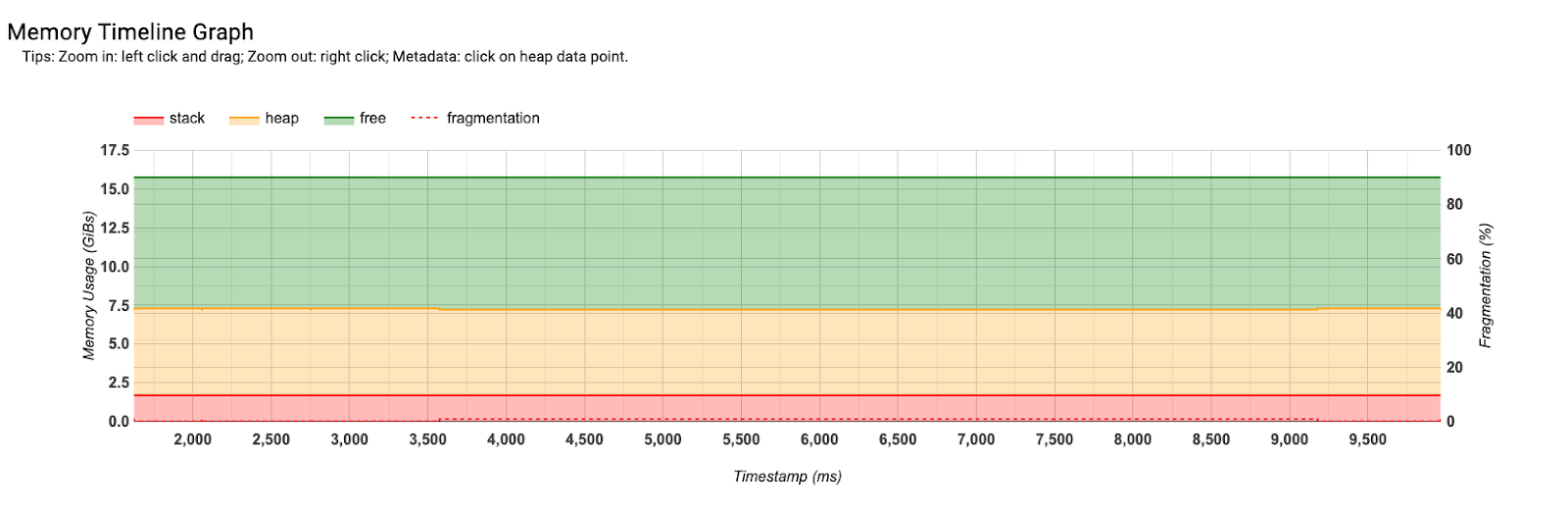
Memory Profile을 사용하면 시간 함수로서의 프로그램 메모리를 쉽게 볼 수 있습니다. 이는 OOM 디버깅에 유용합니다. 여기에서 모델 파라미터에 할당된 약 7.5GB와 약 10GB의 여유 공간을 볼 수 있습니다. 따라서 우리는 메모리에 훨씬 더 많은 것을 넣을 수 있습니다.

Worked Problems

Question 1: 이 Colab/profile을 살펴보고 무엇이 의심스럽고 무슨 일이 일어나고 있는지 파악해 보세요. 어떤 계산이 일어나고 있고 각 작업이 무엇을 하고 있는지 정확히 말할 수 있나요? 관련된 각 행렬의 실제 모양은 무엇이며 어떻게 샤딩되어 있나요? 코드를 읽기 전에 프로파일을 먼저 살펴보세요.

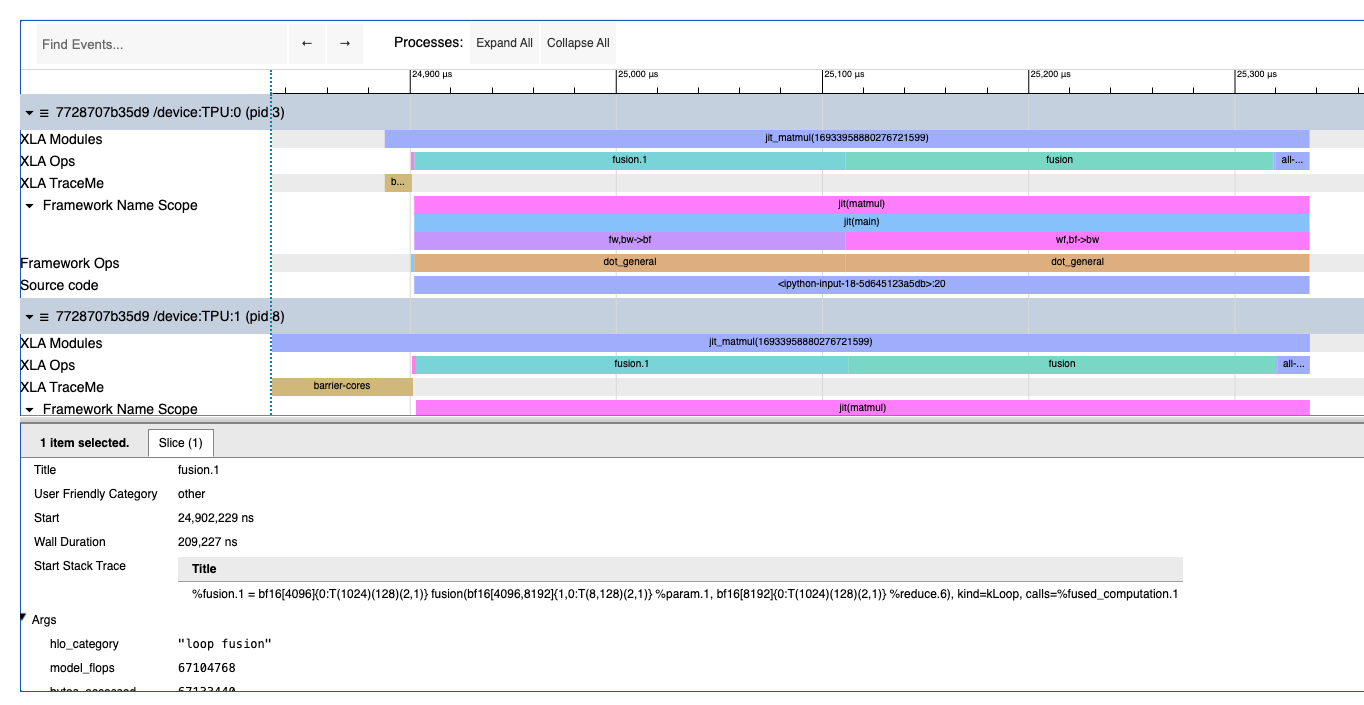
답을 보려면 여기를 클릭하세요.

이것은 두 개의 행렬 곱셈입니다. 구체적으로 다음과 같습니다:

def matmul(w1, w2, x):
  return jnp.einsum('wf,bf->bw', w2, jnp.einsum('fw,bw->bf', w1, x))

Reduce 하나, 큰 fusion 두 개, all-reduce 하나를 볼 수 있습니다. 첫 번째 큰 fusion은 다음과 같습니다:

%fusion.1 = bf16[4096]{0:T(1024)(128)(2,1)} fusion(bf16[4096,8192]{1,0:T(8,128)(2,1)} %param.1, bf16[8192]{0:T(1024)(128)(2,1)} %reduce.6), kind=kLoop, calls=%fused_computation.1

이는 샤드당 형태가 bf16[8192] * bf16[4096, 8192] -> bf16[4096] (8192 차원에 대해)임을 알려줍니다. replica_groups=\{\{0,16,32,48,64,80,96,112\}, ...\}가 있는 최종 AllReduce를 관찰하면 8방향 모델 병렬 처리를 수행하고 있음을 알 수 있으므로, 실제 형태는 [8, 8192] * bf16[32,768, 8192] -> bf16[8, 32,768]입니다.

Question 2: 앞서 언급한 Transformer Colab은 간단한 모의 Transformer를 구현합니다. Colab의 지침에 따라 GSPMD 파티셔닝을 사용하는 순진한 Transformer의 벤치마크를 얻으세요. 각 부분은 얼마나 걸리나요? 얼마나 걸려야 하나요? 어떤 샤딩이 사용되고 있나요? 샤딩을 고쳐보세요! 힌트: 동작을 제약하려면 jax.lax.with_sharding_constraints를 사용하세요. 이 수정으로 얻을 수 있는 최고의 MXU는 무엇인가요?

참고로 초기 버전은 대략 184ms / layer를 얻고 최적화된 프로파일은 67 ms / layer를 얻습니다. 이 작업을 완료한 후 프로파일을 응시하고 다음 질문에 프로파일만으로 답할 수 있는지 확인해 보세요:

이것은 어떤 샤딩 전략인가요?
배치 크기, \(d_\text{model}\), \(d_\text{ff}\)는 무엇인가요?
어텐션 대 MLP 블록에 소비되는 시간의 비율은 얼마인가요?
루프라인에서 각 op에 소비되어야 하는 시간의 비율은 얼마인가요?

Note: 이 문제가 작성된 이후로 XLA 컴파일러가 더 좋아졌습니다. 초기 버전은 이제 대략 90ms / layer이고 최적화된 프로파일은 약 10ms / layer 더 좋을 뿐입니다(80 ms / layer). 여전히 가지고 놀면서 더 잘할 수 있는지 확인해 볼 가치가 있습니다.

파트 9는 여기까지입니다. JAX 병렬 처리에 대해 자세히 알아보는 파트 10을 보려면 여기를 클릭하세요.

Miscellaneous

^*Work done at Google DeepMind, now at MatX.

Citation

For attribution in academic contexts, please cite this work as:

    Austin et al., "How to Scale Your Model", Google DeepMind, online, 2025.

or as a BibTeX entry:

    @article{scaling-book,
      title = {How to Scale Your Model},
      author = {Austin, Jacob and Douglas, Sholto and Frostig, Roy and Levskaya, Anselm and Chen, Charlie and Vikram, Sharad
      and Lebron, Federico and Choy, Peter and Ramasesh, Vinay and Webson, Albert and Pope, Reiner},
      publisher = {Google DeepMind},
      howpublished = {Online},
      note = {Retrieved from https://jax-ml.github.io/scaling-book/},
      year = {2025}
    }