Sharded Matrices and How to Multiply Them

Part 3 of How To Scale Your Model (Part 2: TPUs | Part 4: Transformer Math)

대규모 ML 모델을 훈련할 때는 파라미터나 입력을 여러 가속기에 걸쳐 분할(또는 '샤딩(sharding)')해야 합니다. LLM은 대부분 행렬 곱셈으로 이루어져 있으므로, 이를 이해하는 것은 결국 행렬이 여러 디바이스에 분할되어 있을 때 어떻게 곱하는지를 이해하는 것으로 귀결됩니다. 저희는 TPU 통신 기본 연산(primitive)의 비용에 기반한 샤딩된 행렬 곱셈의 간단한 이론을 개발합니다.

번역 안내: 원저자(Jacob Austin)의 허락을 받아 원문을 번역 중입니다.
해당 글의 1인칭은 원문 저자를 지칭합니다.
원문: How to Scale Your Model
번역: 신종훈

Partitioning Notation and Collective Operations

수만 개의 TPU나 GPU에서 LLM을 훈련할 때도, 추상적으로는 하나의 가속기에서 훈련할 때와 동일한 계산을 수행합니다. 차이점은 우리의 배열이 단일 TPU/GPU의 HBM에 들어가지 않아서 분할해야 한다는 것입니다.속도를 위해 병렬화를 선택할 수도 있다는 점은 주목할 가치가 있습니다. 더 적은 수의 칩에 넣을 수 있더라도, 더 많은 칩으로 확장하면 단순히 더 많은 FLOPs/s를 얻을 수 있습니다. 예를 들어, 추론 중에는 더 작은 토폴로지에 맞출 수 있지만 지연 시간을 줄이기 위해 더 큰 토폴로지로 확장하기도 합니다. 마찬가지로, 훈련 중에는 스텝 시간을 줄이기 위해 더 많은 칩으로 확장하는 경우가 많습니다. 우리는 이를 배열을 “샤딩(sharding)” 또는 “파티셔닝(partitioning)“한다고 말합니다. 스케일링의 예술은 계산이 효율적으로 유지되도록 모델을 샤딩하는 방법을 알아내는 것입니다.

다음은 4개의 TPU에 걸쳐 샤딩된 2D 배열 A의 예입니다:

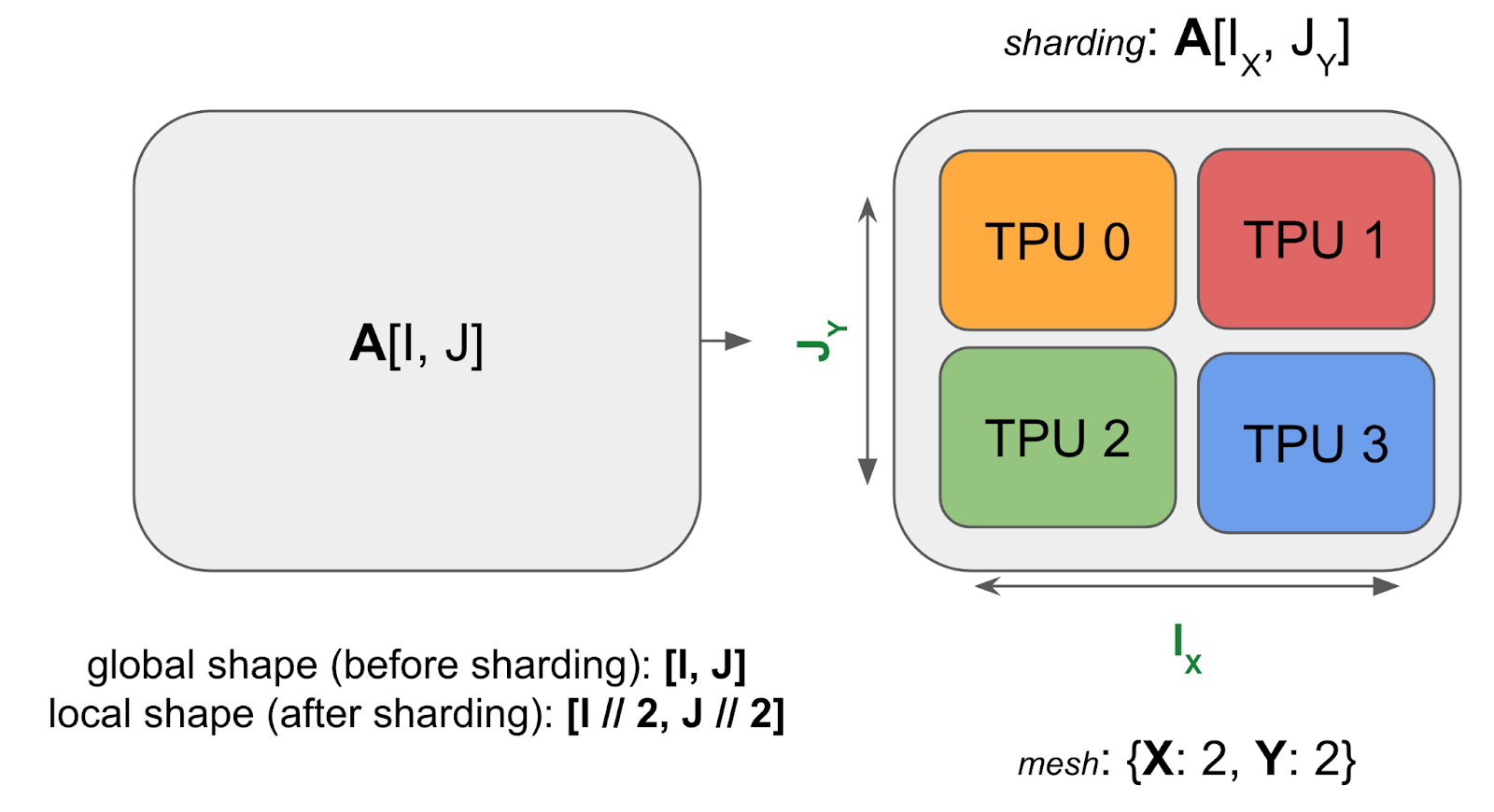
Figure: A[I, J] 형태의 예제 배열이 4개의 디바이스에 걸쳐 샤딩됩니다. 두 차원 모두 A[IX, JY] 샤딩으로 2개의 디바이스에 걸쳐 균등하게 샤딩됩니다. 각 TPU는 전체 메모리의 1/4을 보유합니다.

샤딩된 배열은 여전히 샤딩되지 않은 배열과 동일한 전역(global) 또는 논리적 형태(logical shape)(예: (4, 128))를 가지지만, (2, 64)와 같은 디바이스 로컬 형태(device local shape)도 가집니다. 이는 각 TPU가 실제로 보유하고 있는 바이트 단위의 크기를 알려줍니다(위 그림에서 각 TPU는 전체 배열의 ¼을 보유함). 이제 이를 임의의 배열로 일반화해 보겠습니다.

A unified notation for sharding

우리는 텐서가 디바이스에 걸쳐 블록으로 어떻게 샤딩되는지를 설명하기 위해 named-axis notation의 변형을 사용합니다: X, Y, Z와 같이 메시 축 이름(mesh axis names)이 부여된 2D 또는 3D 디바이스 그리드인 디바이스 메시(device mesh)가 있다고 가정합니다. 그런 다음 배열의 각 이름 있는 차원이 물리적 메시 축에 걸쳐 어떻게 분할되는지를 설명함으로써 행렬 데이터가 디바이스 메시에 어떻게 배치되는지를 지정할 수 있습니다. 우리는 이 할당을 샤딩(sharding)이라고 부릅니다.

예제 (위 다이어그램): 위 다이어그램의 경우, 다음과 같습니다:

이 둘을 종합하면, 배열의 로컬 형태(개별 디바이스가 보유하는 샤드의 크기)는 $(\lvert I\rvert / 2, \lvert J\rvert / 2)$ 임을 알 수 있습니다. 여기서 \(\lvert I\rvert\)는 A의 첫 번째 차원 크기이고 \(\lvert J\rvert\) 는 A의 두 번째 차원 크기입니다.

Pop Quiz [1개 축에 대한 2D 샤딩]: 샤딩 $A[I_{XY}, J]$와 메시 {'X': 8, 'Y': 2}를 가진 배열 fp32[1024, 4096]을 고려해 봅시다. 각 디바이스가 보유하는 데이터 양은 얼마인가요? H100에서 HBM으로부터 이 배열을 로드하는 데 얼마나 걸릴까요? (칩당 메모리 대역폭은 3.4e12로 가정)

답을 보려면 여기를 클릭하세요.

$A[I_{XY}, J]$는 첫 번째 차원(I)을 X와 Y 하드웨어 축 모두에 걸쳐 샤딩합니다. 이 예제에서 로컬 형태는 $(\lvert I\rvert /(\lvert X\rvert \cdot \lvert Y\rvert), \lvert J\rvert)$입니다. 주어진 전역 형태가 fp32[1024, 4096]이므로, 로컬 형태는 fp32[64, 4096]입니다.

각 GPU는 4 * 64 * 4096 = 1MiB 바이트를 가지므로, 대략 1e6 / 3.4e12 = 294ns가 걸립니다. 하지만 크기가 매우 작기 때문에 다양한 오버헤드로 인해 실제로는 훨씬 더 걸릴 것입니다.

Visualizing these shardings: 4개의 디바이스에 분할된 2D 데이터 배열을 보며 이러한 샤딩을 시각화해 봅시다:

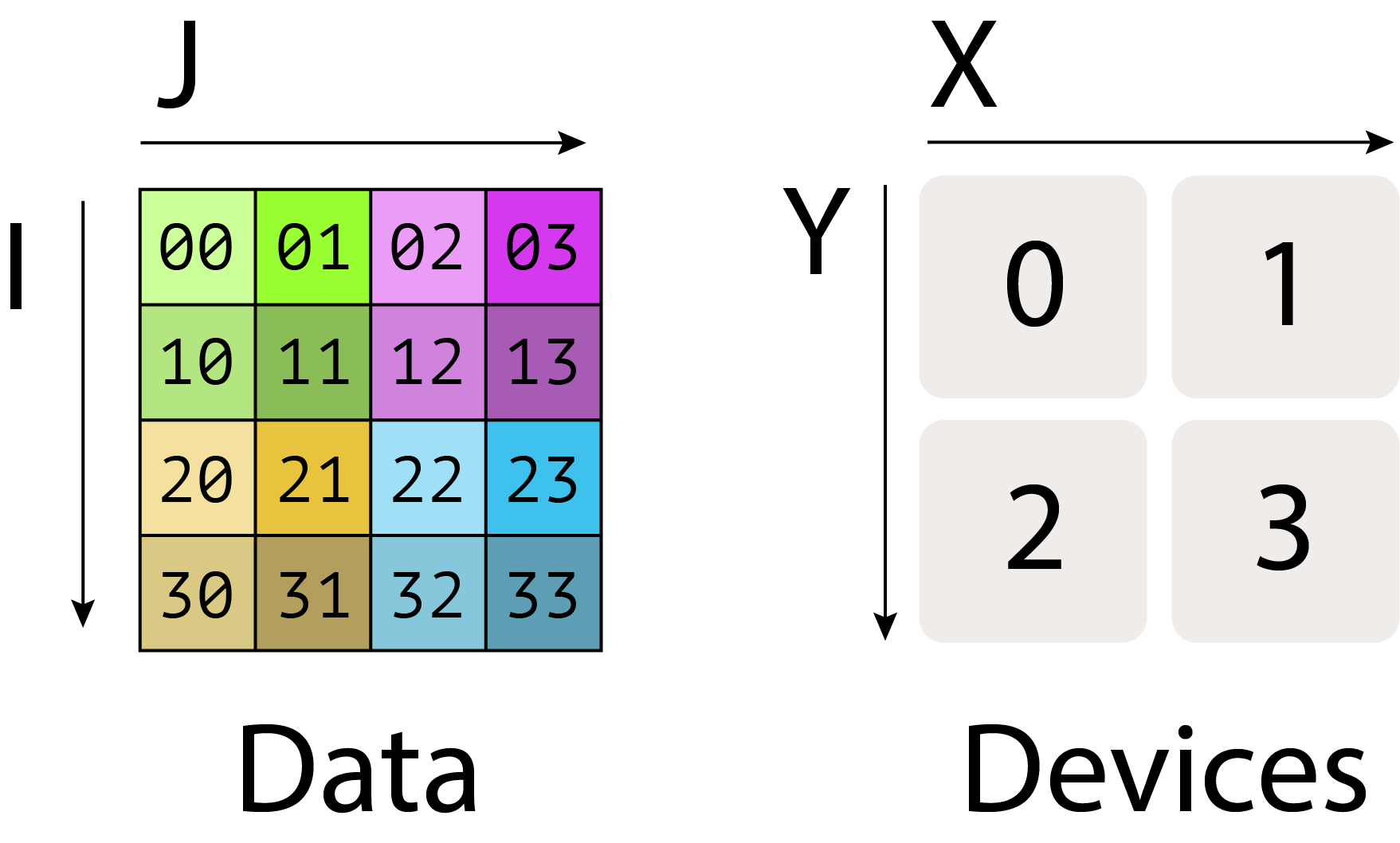
행렬의 완전 복제(fully-replicated) 형태는 샤딩 할당 없이 단순히 $A[I, J]$로 씁니다. 이는 각 디바이스가 전체 행렬의 완전한 복사본을 포함함을 의미합니다.

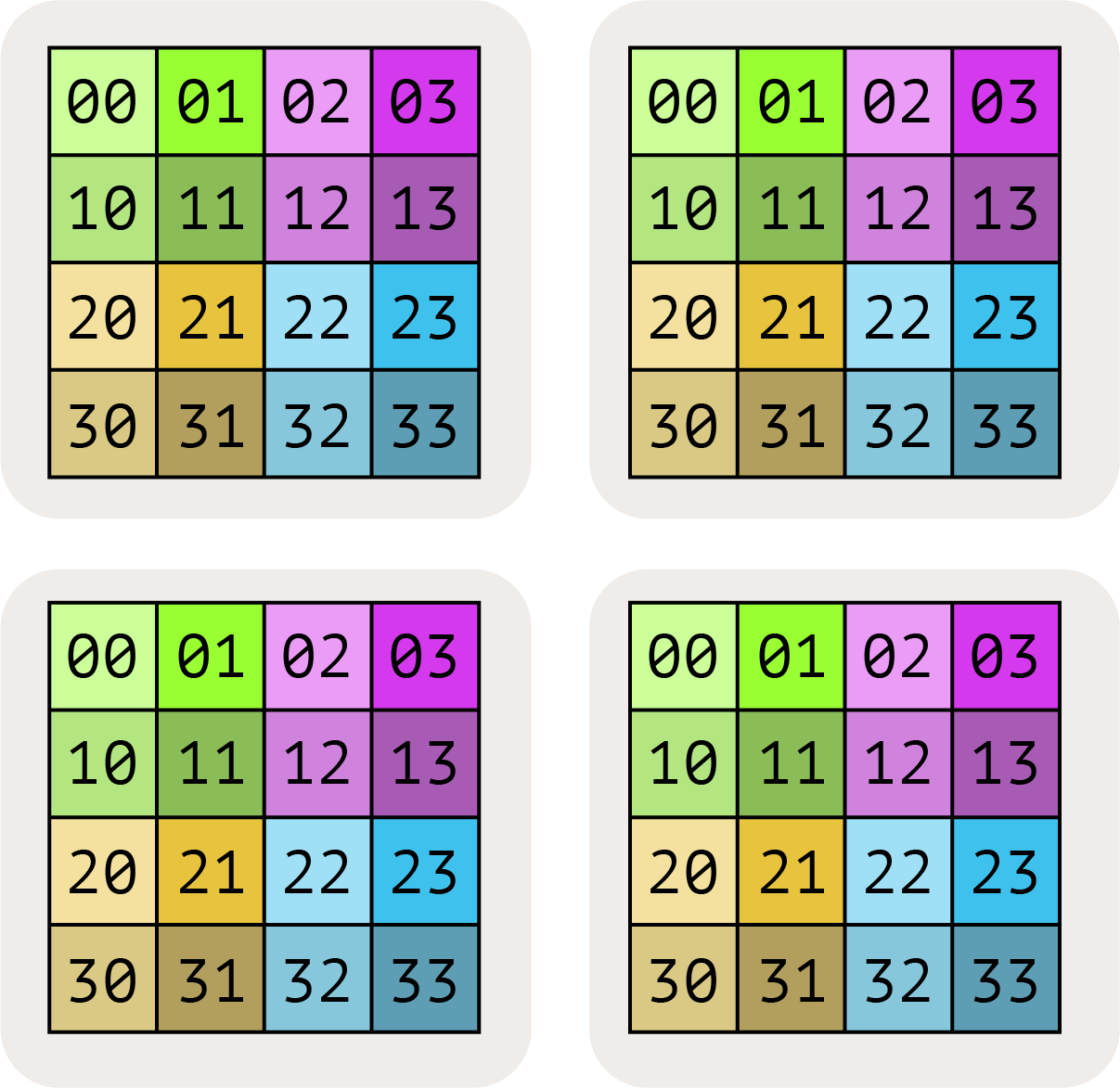
이러한 차원 중 하나가 메시 축에 걸쳐 분할되었음을 나타내고 싶을 때는 메시 축 아래 첨자를 사용합니다. 예를 들어 $A[I_X, J]$는 I 논리적 축이 X 메시 차원에 걸쳐 분할되었지만, J 차원은 분할되지 않았으며, 블록이 Y 메시 축에 걸쳐 부분적으로 복제(partially-replicated)되어 있음을 의미합니다.

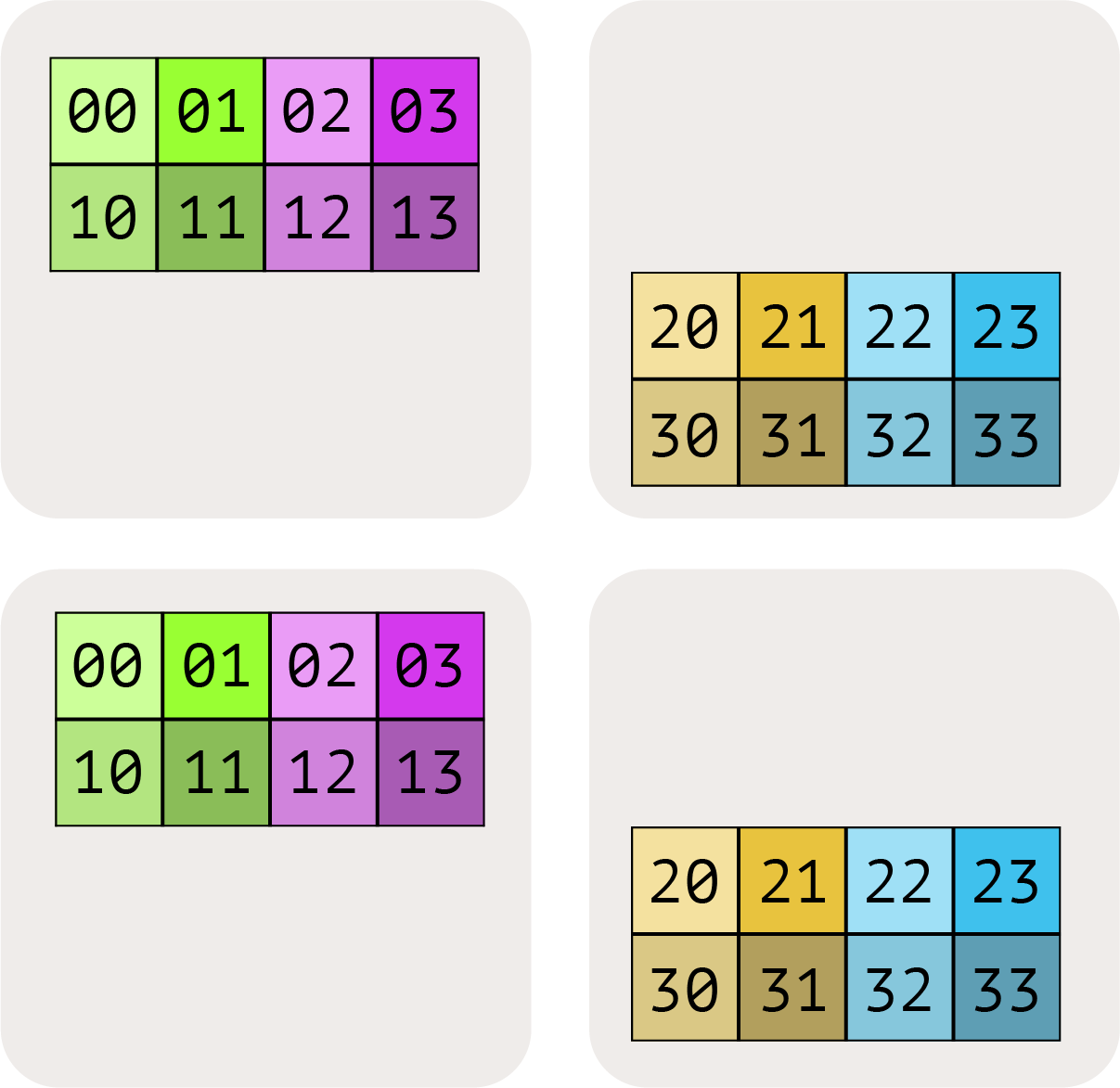
$A[I_X, J_Y]$ 는 I 논리적 축이 X 메시 축에 걸쳐 분할되었고, J 차원이 Y 메시 축에 걸쳐 분할되었음을 의미합니다.

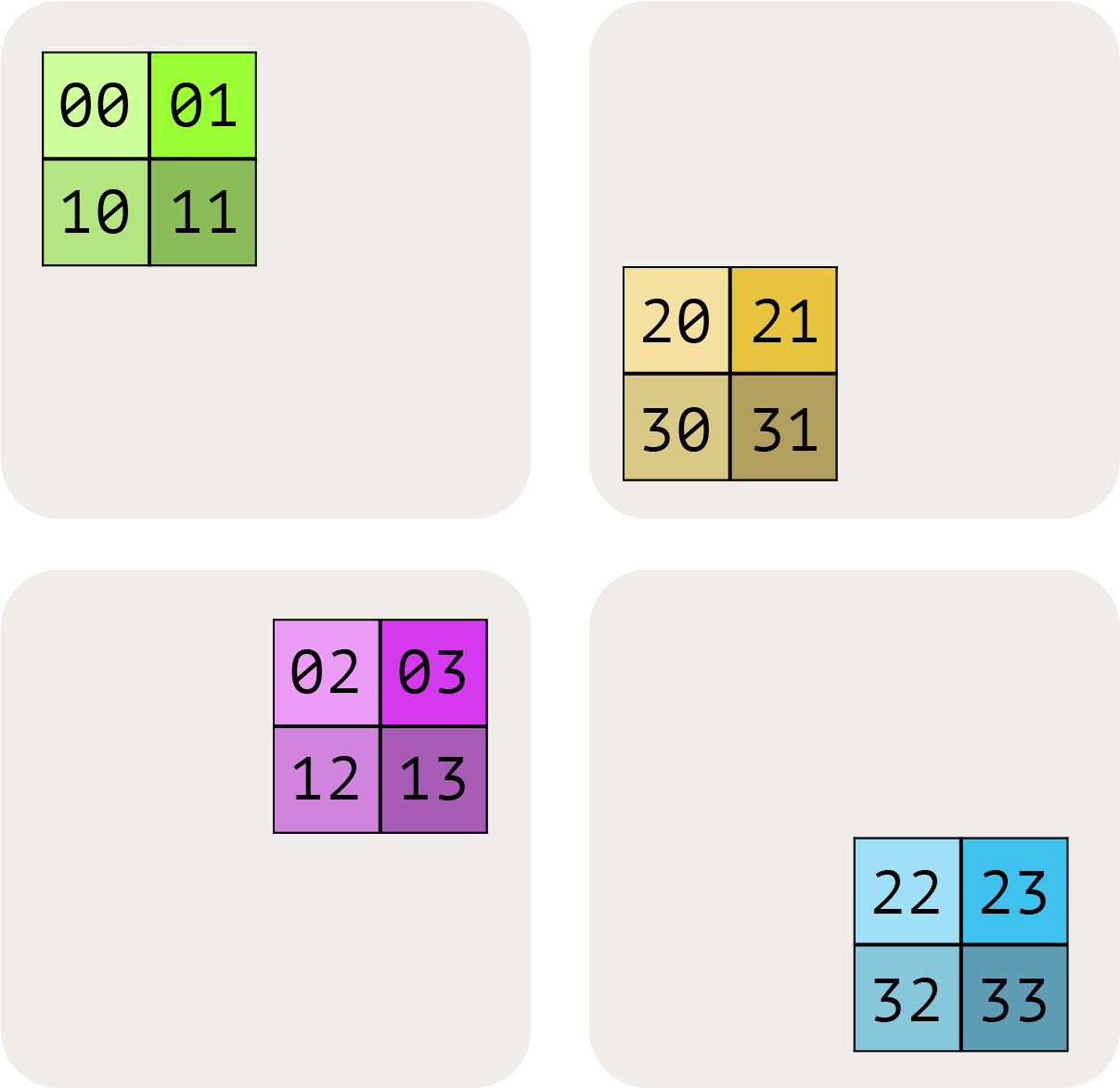
아래 그림에서 다른 가능성들을 보여줍니다:

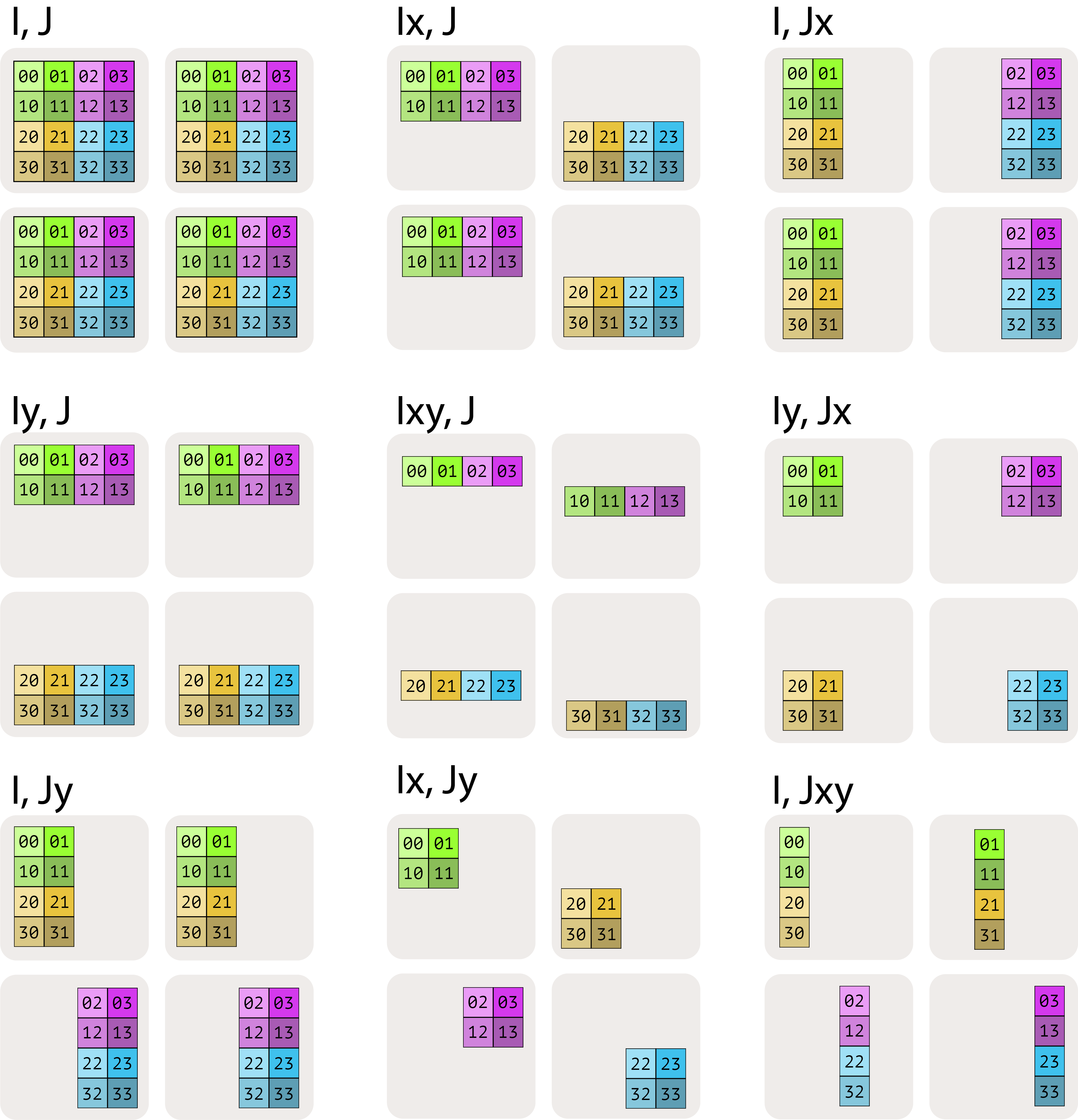
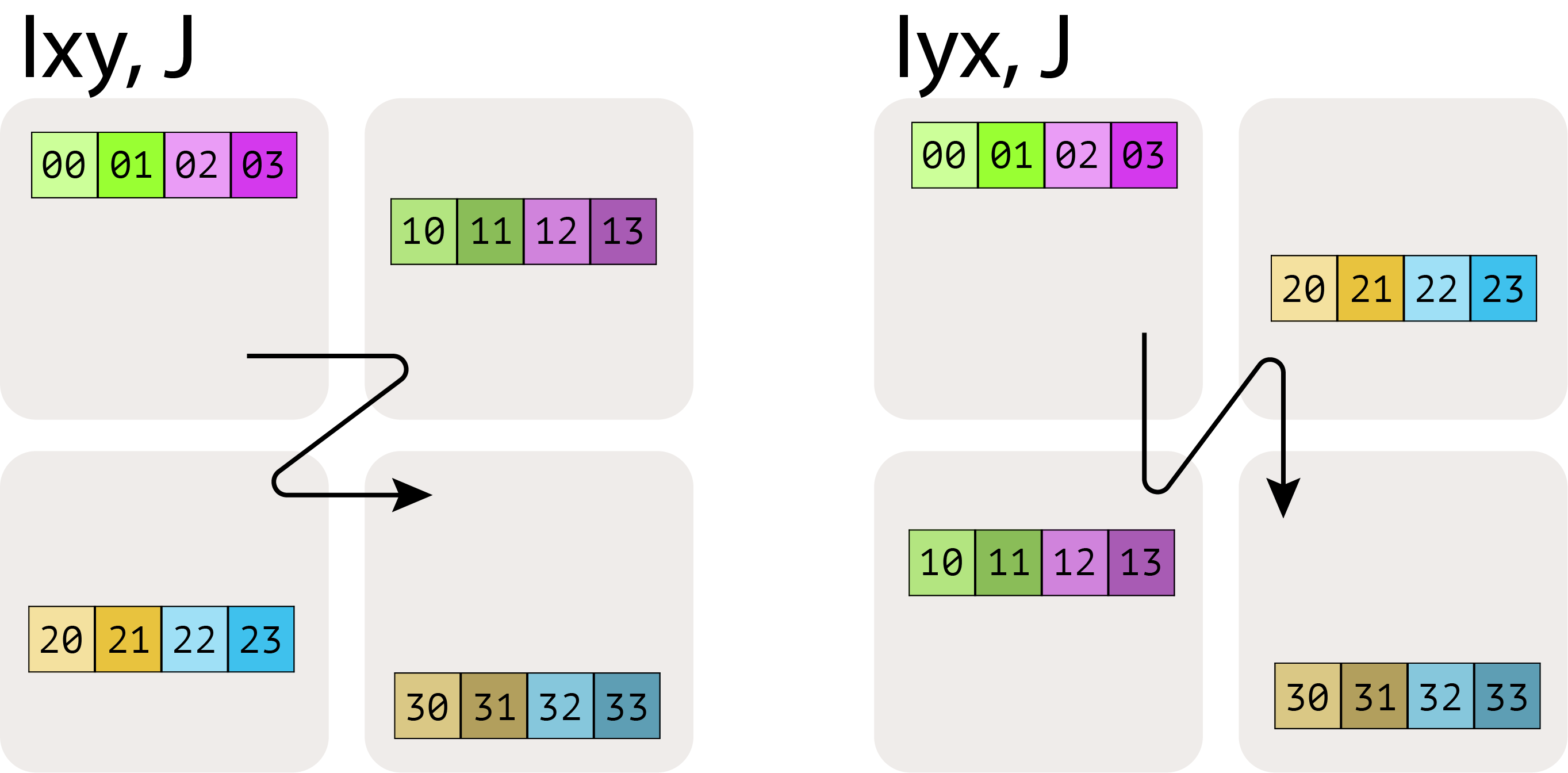
여기서 $A[I_{XY}, J]$ 는 X와 Y 메시 축을 더 큰 평탄화된 차원으로 취급하고, I 이름 있는 축을 모든 디바이스에 걸쳐 분할함을 의미합니다. 여러 메시 축 아래 첨자의 순서는 그리드에 걸친 분할(partitioning)의 순회 순서(traversal order)를 지정하므로 중요합니다.

마지막으로, 여러 이름 있는 축이 동일한 메시 차원을 따라 샤딩될 수 없다는 점에 유의하세요. 예를 들어 $A[I_X, J_X]$는 의미가 없는 금지된 샤딩입니다. 메시 차원이 배열의 한 차원을 샤딩하는 데 사용되면, 그것은 일종의 “소진된” 상태가 됩니다.

Pop Quiz: A가 int8[128, 2048] 형태의 배열이고, 샤딩이 $A[I_{XY}, J]$이며, 메시가 Mesh({‘X': 2, ‘Y': 8, ‘Z': 2})(총 32개 디바이스)라고 가정한다면, A는 디바이스당 얼마나 많은 메모리를 사용할까요? 모든 디바이스에 걸쳐 총 얼마나 많은 메모리를 사용할까요?

답을 보려면 여기를 클릭하세요.

Answer: 배열 A는 X와 Y에 걸쳐 샤딩되고 Z에 걸쳐 복제되므로, 디바이스당 형태는 int8[128 / (2 * 8), 2048] = int8[8, 2048]이며, 크기는 8 * 2048 = 16,384 바이트입니다. Z에 걸쳐 복제되므로, X와 Y에 걸쳐 완전히 샤딩된 Z-평면마다 복사본이 하나씩 있고, 그런 평면이 2개 있으므로, 총 크기(모든 디바이스에 걸쳐)는 128 * 2048 * 2 = 512kiB입니다. 또는 32개 디바이스 × 디바이스당 16,384 바이트 = 512 KiB로 확인할 수도 있습니다.

How do we describe this in code?

How do we describe this in code?

JAX는 위에서 설명한 추상적인 구문과 매우 유사한 이름 있는 샤딩 구문을 사용합니다. 이에 대해서는 섹션 10에서 더 자세히 이야기하겠지만, 간단히 미리 살펴보겠습니다. 여기 구글 Colab에서 이것을 직접 실행해보고 결과를 프로파일링하여 JAX가 다른 샤딩을 어떻게 처리하는지 볼 수 있습니다. 이 스니펫은 3가지 작업을 수행합니다:

  1. 8개의 TPU를 ‘X’와 ‘Y’라는 이름이 할당된 두 축을 가진 4x2 그리드로 매핑하는 jax.Mesh를 생성합니다.
  2. 행렬 A와 B를 생성하는데, A는 두 차원 모두에 걸쳐 샤딩되고 B는 출력 차원을 따라 샤딩됩니다.
  3. 샤딩된 배열을 반환하는 간단한 행렬 곱셈을 컴파일하고 수행합니다.
import jax
import jax.numpy as jnp

# Create our mesh! We're running on a TPU v2-8 4x2 slice with names 'X' and 'Y'.
assert len(jax.devices()) == 8
mesh = jax.make_mesh(axis_shapes=(4, 2), axis_names=('X', 'Y'))

# A little utility function to help define our sharding. A PartitionSpec is our
# sharding (a mapping from axes to names).
def P(*args):
  return jax.NamedSharding(mesh, jax.sharding.PartitionSpec(*args))

# We shard both A and B over the non-contracting dimension and A over the contracting dim.
A = jnp.zeros((8, 2048), dtype=jnp.bfloat16, device=P('X', 'Y'))
B = jnp.zeros((2048, 8192), dtype=jnp.bfloat16, device=P(None, 'Y'))

# We can perform a matmul on these sharded arrays! out_shardings tells us how we want
# the output to be sharded. JAX/XLA handles the rest of the sharding for us.
y = jax.jit(lambda A, B: jnp.einsum('BD,DF->BF', A, B), out_shardings=P('X', 'Y'))(A, B)

JAX의 멋진 점은 이 배열들이 샤딩되지 않은 것처럼 동작한다는 것입니다! B.shape는 전역 또는 논리적 형태(2048, 8192)를 알려줄 것입니다. 로컬로 어떻게 샤딩되었는지 보려면 B.addressable_shards를 실제로 봐야 합니다. 이 배열들에 대해 연산을 수행하면 JAX는 연산을 수행하기 위해 어떻게 브로드캐스트하거나 재구성할지 알아서 처리합니다. 예를 들어, 위 예에서 A의 로컬 형태는 [2, 1024]이고 B의 로컬 형태는 [2048, 4096]입니다. JAX/XLA는 최종 곱셈을 수행하기 위해 필요에 따라 이 배열들 간의 통신을 자동으로 추가합니다.

Computation With Sharded Arrays

여러 디바이스에 분산된 데이터 배열이 있고 이에 대해 수학적 연산을 수행하고자 할 때, 데이터와 계산을 모두 샤딩하는 데 관련된 오버헤드는 무엇일까요?

당연히, 이것은 관련된 계산에 따라 다릅니다.

이 섹션의 나머지 부분에서는 샤딩된 행렬을 곱하는 방법을 다룹니다. 대략적으로 말해, 이것은 각 청크를 완전히 곱하거나 합산할 수 있도록 행렬의 청크를 이동시키는 것을 포함합니다. 각 샤딩은 다른 통신을 포함합니다. 예를 들어, $A[I_X, J] \cdot B[J, K_Y] \to C[I_X, K_Y]$는 축소 차원(실제로 합산하는 차원인 J)이 샤딩되지 않았기 때문에 통신 없이 곱셈이 가능합니다. 하지만 출력이 샤딩되지 않기를 원한다면(즉, $A[I_X, J] \cdot B[J, K_Y] \to C[I, K]$), $A$와 $B$ 또는 $C$를 모든 디바이스에 복사해야 합니다(AllGather 사용). 이 두 가지 선택은 다른 통신 비용을 가지므로, 이 비용을 계산하고 가장 낮은 것을 선택해야 합니다.

이를 “블록 행렬 곱셈”으로 생각할 수 있습니다.

먼저 “블록 행렬”, 즉 행렬의 중첩된 행렬 개념을 상기해 봅시다:

\[\begin{equation} \begin{pmatrix} a_{00} & a_{01} & a_{02} & a_{03} \\ a_{10} & a_{11} & a_{12} & a_{13} \\ a_{20} & a_{21} & a_{22} & a_{23} \\ a_{30} & a_{31} & a_{32} & a_{33} \end{pmatrix} = \left( \begin{matrix} \begin{bmatrix} a_{00} & a_{01} \\ a_{10} & a_{11} \end{bmatrix} \\ \begin{bmatrix} a_{20} & a_{21} \\ a_{30} & a_{31} \end{bmatrix} \end{matrix} \begin{matrix} \begin{bmatrix} a_{02} & a_{03} \\ a_{12} & a_{13} \end{bmatrix} \\ \begin{bmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{bmatrix} \end{matrix} \right) = \begin{pmatrix} \mathbf{A_{00}} & \mathbf{A_{01}} \\ \mathbf{A_{10}} & \mathbf{A_{11}} \end{pmatrix} \end{equation}\]

행렬 곱셈은 피곱셈 행렬이 블록으로 작성될 때, 곱이 표준 규칙에 따라 블록 행렬 곱셈으로 작성될 수 있다는 좋은 속성을 가집니다:

\[\begin{equation} \begin{pmatrix} A_{00} & A_{01} \\ A_{10} & A_{11} \end{pmatrix} \cdot \begin{pmatrix} B_{00} & B_{01} \\ B_{10} & B_{11} \end{pmatrix} = \begin{pmatrix} A_{00}B_{00} + A_{01}B_{10} & A_{00}B_{01} + A_{01}B_{11} \\ A_{10}B_{00} + A_{11}B_{10} & A_{10}B_{01} + A_{11}B_{11} \end{pmatrix} \end{equation}\]

이것이 의미하는 바는, 분산 행렬 곱셈을 구현하는 것은 이 샤딩된 블록들을 네트워크를 통해 이동시키고, 블록에 대해 로컬 행렬 곱셈을 수행하고, 그 결과를 합산하는 것으로 귀결된다는 것입니다. 문제는 어떤 통신을 추가하고, 그것이 얼마나 비싼가입니다.

편리하게도, 모든 가능한 샤딩을 우리가 고려해야 할 대략 4가지 경우로 요약할 수 있으며, 각각은 어떤 통신을 추가해야 하는지에 대한 규칙을 가집니다.

  1. Case 1: 어느 피곱셈 행렬도 축소 차원이 샤딩되지 않음. 통신 없이 로컬 샤드를 곱할 수 있습니다.
  2. Case 2: 한 피곱셈 행렬에 샤딩된 축소 차원이 있음. 일반적으로 축소 차원을 따라 샤딩된 입력을 “AllGather”합니다.
  3. Case 3: 두 피곱셈 행렬 모두에 샤딩된 축소 차원이 있음. 로컬 샤드를 곱한 다음, 결과를 “AllReduce”할 수 있습니다.
  4. Case 4: 두 피곱셈 행렬 모두 동일한 축을 따라 샤딩된 비축소 차원을 가짐. 두 입력 중 하나를 먼저 AllGather하지 않고는 진행할 수 없습니다.

이것들을 단순히 따라야 할 규칙으로 생각할 수도 있지만, 이 규칙들이 왜 성립하고 얼마나 비싼지를 이해하는 것도 가치가 있습니다. 이제 각각을 자세히 살펴보겠습니다.

Case 1: 어느 피곱셈 행렬도 샤딩된 축소 차원을 가지지 않음

Lemma: 분할된 텐서를 곱할 때, 계산은 유효하며 출력은 입력의 샤딩을 따릅니다. 단, 축소 차원이 샤딩되거나 두 텐서 모두 동일한 축을 따라 샤딩된 비축소 차원을 가지는 경우는 예외입니다. 예를 들어, 다음은 잘 작동합니다.

\[\begin{equation*} \mathbf{A}[I_X, J] \cdot \mathbf{B}[J, K_Y] \rightarrow \mathbf{C}[I_X, K_Y] \end{equation*}\]

전혀 통신 없이, 그리고 결과는 X와 Y 하드웨어 차원 모두에 걸쳐 샤딩된 텐서가 됩니다. 왜 그런지 생각해보세요. 기본적으로, 계산은 샤딩과 독립적입니다. 왜냐하면 각 배치 항목은 곱하고 축소할 수 있는 축소 중인 축의 로컬 청크를 가지고 있기 때문입니다. 다음 사례들 중 어떤 것이든 잘 작동하며 이 규칙을 따릅니다:

\[\begin{align*} \mathbf{A}[I, J] \cdot \mathbf{B}[J, K] \rightarrow &\ \mathbf{C}[I, K] \\ \mathbf{A}[I_X, J] \cdot \mathbf{B}[J, K] \rightarrow &\ \mathbf{C}[I_X, K]\\ \mathbf{A}[I, J] \cdot \mathbf{B}[J, K_Y] \rightarrow &\ \mathbf{C}[I_X, K_Y]\\ \mathbf{A}[I_X, J] \cdot \mathbf{B}[J, K_Y] \rightarrow &\ \mathbf{C}[I_X, K_Y] \end{align*}\]

A나 B 모두 샤딩된 축소 차원 J를 가지지 않으므로, 입력의 로컬 블록 행렬 곱셈을 수행하기만 하면 결과는 이미 원하는 출력 샤딩에 따라 샤딩되어 있습니다. 두 피곱셈 행렬 모두 동일한 축을 따라 샤딩된 비축소 차원을 가질 때는 이것이 더 이상 사실이 아닙니다(invalid shardings(유효하지 않은 샤딩) 섹션 참조).

Case 2: 한 피곱셈 행렬이 샤딩된 축소 차원을 가짐

축소 J 차원에서 샤딩된 A와 완전 복제된 B의 분산 행렬 곱셈의 간단한 경우를 고려해 봅시다:

\[\mathbf{A}[I, J_X] \cdot \mathbf{B}[J, K] \rightarrow \mathbf{C}[I, K]\]

로컬 A, B 블록을 서로 곱하는 로컬 행렬 곱셈을 단순히 수행할 수 없습니다. A의 축소 축에서 전체 데이터가 없기 때문입니다. 일반적으로, 먼저 A의 샤드를 로컬에서 “AllGather“한 다음, B와 곱합니다:

\[\textbf{AllGather}_X[I, J_X] \rightarrow \mathbf{A}[I, J]\] \[\mathbf{A}[I, J] \cdot \mathbf{B}[J, K] \rightarrow \mathbf{C}[I, K]\]

AllGather는 축을 따라 샤딩을 제거하고 디바이스에 걸쳐 퍼져 있는 샤드를 해당 축을 따라 각 디바이스에 재조립합니다. 위 표기법을 사용하면, AllGather는 축 집합에서 아래 첨자를 제거합니다. 예:

\[\textbf{AllGather}_{XY}(A[I_{XY}, J]) \rightarrow A[I, J]\]

주어진 차원에 대해 모든 아래 첨자를 제거할 필요는 없습니다. 예: \(A[I_{XY}, J] \rightarrow A[I_Y, J]\) 도 단일 축에 대한 AllGather입니다.

non-contracting(비축소) 차원 샤딩을 제거하기 위해 AllGather를 사용할 수도 있습니다. 예를 들어, 행렬 곱셈:

\[A[I_X, J] \cdot B[J, K] \rightarrow C[I, K]\]

출력 샤딩을 제거하기 위해 유사하게 X를 따라 AllGather를 수행할 수 있습니다. 하지만 축소 차원을 AllGather하는 경우와는 달리, 이 경우에는 행렬 곱셈을 수행하기 전이나 후에 AllGather를 할 수 있습니다. 축소 차원은 반드시 행렬 곱셈을 수행하기 전에 AllGather해야 합니다.

AllGather는 실제로 어떻게 수행될까요? 단일 축을 따라 1차원 AllGather를 수행하려면, 모든 디바이스가 복사본을 가질 때까지 모든 샤드를 축 링(ring) 주위로 전달해야 합니다.GPU AllGather도 이와 같이 작동할 수 있는데, 노드 내 GPU들로 링을 만들고 청크를 (임의의) 순서로 전달합니다. 다음은 애니메이션입니다:

Figure: 8개의 TPU 또는 GPU 디바이스 세트 주위로 AllGather를 수행하는 방법을 보여주는 애니메이션. 각 디바이스는 배열의 1/8로 시작하여 전체 복사본으로 끝납니다.

AllGather는 한 방향 또는 양방향으로 수행할 수 있습니다(위 그림은 두 방향을 보여줍니다). 한 방향으로 하면 각 TPU가 \(\text{bytes} / N\)크기의 청크를 링 주위로\(N - 1\)홉만큼 보냅니다. 두 방향으로 하면\(2 \cdot \text{bytes} / N\) 크기의 홉이 $\lfloor \frac{N}{2} \rfloor$ 번 필요합니다.

이것은 얼마나 오래 걸릴까요? 양방향 AllGather를 예로 들어 얼마나 오래 걸리는지 계산해 봅시다. \(V\)를 배열의 바이트 수, \(X\)를 축소 차원의 샤드 수라고 합시다. 위 다이어그램에서 각 홉은 각 방향으로 $V / \lvert X\rvert$ 바이트를 보내므로, 각 홉은 다음과 같은 시간이 걸립니다.

\(T_{hop} = \frac{2 \cdot V}{X \cdot W_\text{ici}}\) \(T_{hop} = \frac{2 \cdot V}{X \cdot W_\text{ici}}\)

여기서 \(W_\text{ici}\)는 양방향(bidirectional) ICI 대역폭입니다.분자의 2는 양방향 대역폭을 사용하고 있다는 사실에서 비롯됩니다. 각 방향으로 $V / X$를 보내므로 총 $2V / X$를 보냅니다. 모든 TPU에 도달하기 위해 총 $\lvert X\rvert / 2$ 홉을 보내야 하므로기술적으로는 $\lfloor X / 2 \rfloor$, 전체 축소에는 다음과 같은 시간이 걸립니다.

\(T_{total} = \frac{2 \cdot V \cdot X}{2 \cdot X \cdot W_\text{ici}}\) \(T_{total} = \frac{2 \cdot V \cdot X}{2 \cdot X \cdot W_\text{ici}}\)

\[T_{total} = \frac{V}{W_\text{ici}}\]

이것이 \(X\)에 의존하지 않는다는 점에 유의하세요! 이는 꽤 놀라운 사실인데, 왜냐하면 우리 TPU가 로컬로만 연결되어 있음에도 불구하고 연결의 지역성이 중요하지 않다는 것을 의미하기 때문입니다. 우리는 단지 각 링크의 속도에 의해 병목 현상을 겪습니다.

Takeaway: throughput-bound 환경에서 AllGather(또는 ReduceScatter나 AllReduce)를 수행할 때, 실제 통신 시간은 배열이 샤딩된 디바이스의 수가 아니라 배열의 크기와 사용 가능한 대역폭에만 의존합니다!

ICI 지연 시간에 대한 참고 사항: ICI 링크를 통한 각 홉은 데이터 양과 관계없이 고유한 오버헤드를 가집니다. 이는 보통 약 1us입니다. 이는 배열 \(A\)가 매우 작고 각 홉이 1us 미만으로 걸릴 때, 계산이 \(X\)에 의존하는 “지연 시간 제한적인(latency-bound)” 환경에 들어갈 수 있음을 의미합니다.

자세한 내용은 여기를 클릭하세요.

\(T_\text{min}\) 을 단일 홉의 최소 시간이라고 합시다. 이 경우에

\(T_{hop} = \max \left[ T_{min}, \frac{2 \cdot V}{X \cdot W_\text{ici}} \right]\) \(T_{hop} = \max \left[ T_{min}, \frac{2 \cdot V}{X \cdot W_\text{ici}} \right]\)

\(T_{total} = \max \left[ \frac{T_{min} \cdot X}{2}, \frac{V}{W_\text{ici}} \right]\) \(T_{total} = \max \left[ \frac{T_{min} \cdot X}{2}, \frac{V}{W_\text{ici}} \right]\)

이 됩니다. 왜냐하면 우리는 \(X / 2\) 홉을 수행하기 때문입니다. 큰 축소나 수집의 경우, 우리는 확실히 대역폭 제한적입니다. 너무 많은 데이터를 보내고 있어서 각 홉의 오버헤드는 거의 무시할 수 있습니다. 하지만 작은 배열(예: 모델에서 샘플링할 때)의 경우, 이는 무시할 수 없으며 ICI 대역폭은 관련이 없습니다. 우리는 순수하게 지연 시간에 의해 제한됩니다. 다른 말로 하면, 특정 TPU(예: 4.5e10 단방향 ICI 대역폭을 가진 TPU v5e)가 주어졌을 때, 4.5e10 * 1e-6 = 45kB 미만의 버퍼를 보내는 것은 지연 시간 제한적이 될 것입니다.

다음은 TPU v5e 8x16 슬라이스에서 AllGather 대역폭을 실증적으로 측정한 것입니다. 배열은 16개 축에 걸쳐 샤딩되어 완전한 양방향 링을 가집니다.

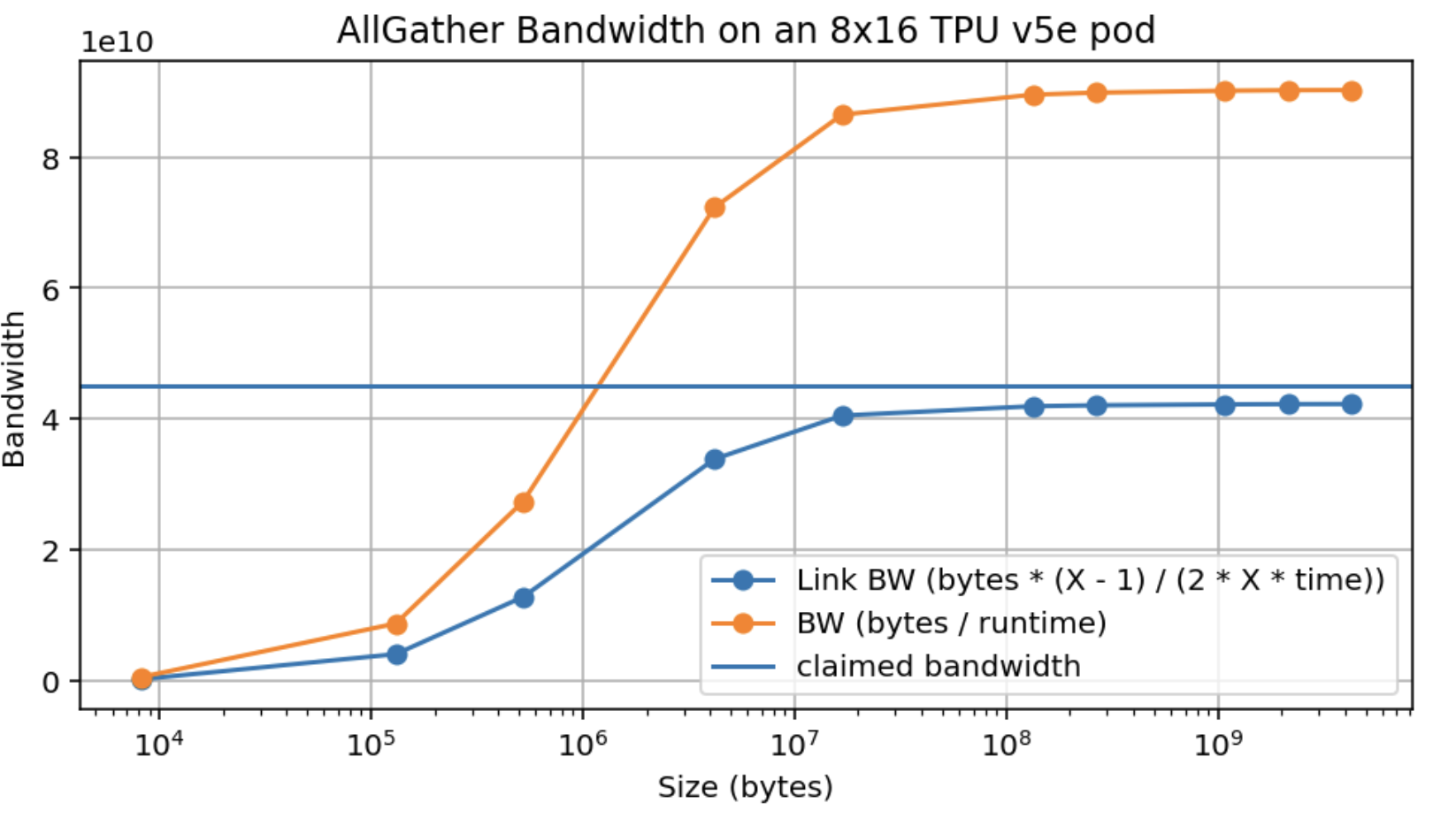
Figure: AllGather 중 TPU v5e의 실증적 대역폭 및 추정 링크 대역폭. 주황색 BW는 AllGather된 실제 초당 바이트 수이며, 파란색 곡선은 집합 연산의 알려진 비용에 따라 계산된 실증적 단방향 링크 대역폭을 보여줍니다.

주장된 최대 대역폭(4.5e10)의 약 95%만 달성하고, 이 최대치를 약 10MB에서만 달성한다는 점에 유의하세요. 16방향으로 샤딩되면 디바이스당 약 500kB가 됩니다(참고: 이는 GPU보다 훨씬 낫습니다).

여러 축에 걸쳐 AllGather를 수행하면 어떻게 될까요? 여러 축에 걸쳐 수집할 때, 우리는 수집을 수행할 여러 차원의 ICI를 가집니다. 예를 들어, AllGatherXY([B, DXY])는 두 개의 하드웨어 메시 축에 걸쳐 작동합니다. 이는 사용 가능한 대역폭을 \(N_\text{axes}\) 배만큼 증가시킵니다.

지연 시간을 고려할 때, 우리는 다음과 같은 일반적인 규칙을 얻습니다:

\[T_{total} = \max \left[ \frac{T_{min} \cdot \sum_{i} |X_i|}{2}, \frac{V}{W_\text{ici} \cdot N_\text{axes}} \right]\]

여기서 \(\sum_i \lvert X_i \rvert / 2\)는 TPU 메시에서 가장 긴 경로의 길이입니다.

Pop Quiz 2 [AllGather time]: 파트 2의 수치를 사용하여, 2D 메시 {'X': 8, 'Y': 4}를 가진 TPUv5e에서 \(E = 2048\), \(F = 8192\)인 bfloat16의 AllGatherY([EY, F]) → [E, F]를 수행하는 데 얼마나 걸릴까요? \(E=256, F=256\)일 때는 어떨까요?

답을 보려면 여기를 클릭하세요.

Answer: 몇 가지 기본 수를 계산하는 것으로 시작하겠습니다:

1) TPU v5e는 2개의 각 축에 대해 초당 4.5e10 바이트의 단방향 ICI 대역폭을 가집니다. 2) (a)의 bfloat16에서, 우리는 $A[E_Y, F]$를 가지므로 각 디바이스는 bfloat16[512, 8192] 형태의 배열을 보유하며, 이는 512 * 8192 * 2 = 8.4MB의 크기를 가집니다. 전체 배열의 크기는 2048 * 8192 * 2 = 34MB입니다.

파트 (1)의 경우, 위 공식을 사용할 수 있습니다. 한 축에 대해서만 AllGather를 수행하므로, $T_{\text{comms}} = 34e6 / 9e10 = 377\mu s$입니다. latency bound인지 확인하기 위해, 크기 4의 축에서는 최대 3개의 홉이 있으므로 지연 시간 한계는 약 3us 정도이므로 근접하지 않습니다. 하지만 TPU v5e는 한 축의 크기가 16일 때만 랩어라운드 연결을 가지므로, 여기서는 실제로 완전한 양방향 AllGather를 할 수 없습니다. 가장자리에서 다른 가장자리로 데이터가 도달하려면 3개의 홉이 필요하므로, 이론적으로는 $T_{\text{comms}} = 3 * 8.4e6 / 4.5e10 = 560\mu s$에 가깝습니다. 이 Colab의 실제 프로파일 은 $680 \mu s$를 보여주는데, 이는 이론적 대역폭의 100%를 얻지 못할 가능성이 높기 때문에 합리적입니다! 파트 (2)의 경우 각 샤드의 크기는 64 * 256 * 2 = 32kB입니다. 32e3 / 4.5e10 = 0.7us이므로, 우리는 latency bound입니다. 3개의 홉이 있으므로, 대략 3 * 1us = 3us가 걸릴 것입니다. 실제로는 8us에 가깝습니다.

Note: {'X': 16, 'Y': 4}와 같은 2D 메시가 있을 때, 각 축이 특정 하드웨어 축에 대응될 필요는 없습니다. 예를 들어, 위의 내용은 $X$ 축에 2개의 축이 있는 4x4x4 TPU v5p 큐브를 설명할 수도 있습니다. 이는 나중에 여러 축에 걸친 데이터 병렬 처리를 설명할 때 작용합니다.

Case 3: 두 피연산자 모두 축소 차원이 분할된 경우

세 번째 기본 경우는 두 피연산자 모두 동일한 메시 축을 따라 축소 차원에 샤딩된 경우입니다:

\[\textbf{A}[I, J_X] \cdot \textbf{B}[J_X, K] \rightarrow C[I, K]\]

이 경우, 로컬 분할된 블록 행렬 곱셈은 동일한 축소 인덱스 집합을 공유하므로 최소한 수행이 가능합니다. 하지만 각 곱은 원하는 전체 곱의 부분 합만을 나타낼 것이며, X 차원을 따르는 각 디바이스는 이 최종 원하는 곱의 다른 부분 합을 가지게 될 것입니다. 이는 매우 흔한 경우이므로, 이 조건을 명시적으로 표시하기 위해 표기법을 확장합니다:

\[\textbf{A}[I, J_X] \cdot_\text{LOCAL} \textbf{B}[J_X, K] \rightarrow C[I, K] \{\ U_X \}\]

{ UX } 표기법은 “X 메시 축에 대해 축소되지 않음(unreduced)“으로 읽으며, 연산이 최종 합산이 보류된 채 “미완성” 상태임을 의미합니다. $\cdot_\text{LOCAL}$ 구문은 로컬 합계를 수행하지만 결과를 축소되지 않은 상태로 남겨둔다는 것을 의미합니다.

이는 행렬 곱셈과 외적(outer product)에 대한 다음 결과로 볼 수 있습니다:

\[A \cdot B = \sum_{i=1}^{P} \underbrace{A_{:,i} \otimes B_{i,:}}_{\in \mathbb{R}^{n \times m}}\]

여기서 ⊗는 외적(outer product)입니다. 따라서, 축 X의 TPU i가 A의 i번째 열과 B의 i번째 행을 가지고 있다면, 로컬 행렬 곱셈을 수행하여 \(A_{:,i} \otimes B_{i,:} \in \mathbb{R}_{n\times m}\)을 얻을 수 있습니다. 이 행렬의 각 항목에는 A • B가 해당 항목에서 가지는 합의 i번째 항이 포함됩니다. 전체 A • B를 얻으려면 메시 축 X에 걸쳐 샤딩한 P에 대해 여전히 합산을 수행해야 합니다. 이는 A와 B를 블록(즉, 샤드)으로 쓰고 결과의 각 샤드에 대해 합산하는 것과 동일한 방식으로 작동합니다.

이를 완화하기 위해 X 축에 걸쳐 전체 AllReduce를 사용하여 이 합산을 수행할 수 있습니다:

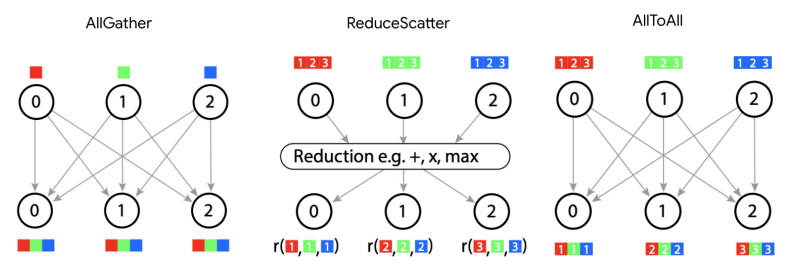
\[\begin{align*} A[I, J_X] \cdot_\text{LOCAL} B[J_X, K] \rightarrow &\ C[I, K] \{ U_X \} \\ \textbf{AllReduce}_X C[I, K] \{ U_X \} \rightarrow &\ C[I, K] \end{align*}\]

AllReduce는 부분 합(partial sums)을 제거하여, 축을 따르는 각 디바이스가 동일한 완전히 합산된 값(fully-summed value)을 갖게 합니다. AllReduce는 이 섹션에서 논의할 몇 가지 핵심 통신 중 두 번째이며, 첫 번째는 AllGather, 다른 것들은 ReduceScatter와 AllToAll입니다. AllReduce는 축소되지 않은(부분적으로 합산된) 축을 가진 배열을 가져와 해당 축 주위로 샤드를 전달하고 결과를 누적하여 합산을 수행합니다. 시그니처는 다음과 같습니다.

\[\textbf{AllReduce}_Y A[I_X, J] \{U_Y\} \rightarrow A[I_X, J]\]

이는 단순히 $\{U_Y\}$ 접미사를 제거하지만 그 외에는 결과를 변경하지 않음을 의미합니다.

AllReduce는 얼마나 비쌀까요? AllReduce가 어떻게 수행되는지에 대한 한 가지 멘탈 모델은 모든 디바이스가 자신의 샤드를 이웃에게 보내고, 받는 모든 샤드를 합산하는 것입니다. 분명히, 각 “샤드”가 전체 배열과 동일한 형태를 가지기 때문에 이는 AllGather보다 더 비쌉니다. 일반적으로, AllReduce는 AllGather보다 두 배 비쌉니다. 이를 확인하는 한 가지 방법은 AllReduce가 다른 두 가지 기본 연산(primitives), 즉 ReduceScatter와 AllGather의 합성으로 표현될 수 있다는 점을 주목하는 것입니다. AllReduce와 마찬가지로, ReduceScatter는 배열의 부분 합을 해결하지만 주어진 차원을 따라 ‘흩뿌려진(scattered)’ 또는 분할된 출력을 생성합니다. AllGather는 이 모든 조각을 모아 해당 물리적 축을 따라 논리적 축을 ‘unpartitions/unshards/replicates’합니다.

\[\begin{align*} \textbf{ReduceScatter}_{Y,J} : A[I_X,J] \{U_Y\} \rightarrow &\ A[I_X, J_Y] \\ \textbf{AllGather}_Y : A[I_X, J_Y] \rightarrow &\ A[I_X, J] \end{align*}\]

ReduceScatter는 어떨까요? AllReduce가 아래 첨자를 제거하는 것처럼($F_Y \to F$ above), ReduceScatter는 축소되지 않은/부분적으로 합산된 배열을 합산한 다음 동일한 메시 축을 따라 다른 논리적 축을 흩뿌립니다(샤딩합니다). $[F]\{U_Y\} \to [F_Y]$. 애니메이션은 이것이 어떻게 수행되는지 보여줍니다: 이는 AllGather와 매우 유사하지만 각 샤드를 유지하는 대신 합산한다는 점에 유의하세요. 따라서, 축소(reduction)를 수행하는 데 걸리는 시간을 제외하면 그 지연 시간(latency)은 거의 동일합니다.

각 홉의 통신 시간은 AllGather와 마찬가지로 샤드당 바이트 수 $V / Y$를 대역폭 $W_\text{ici}$로 나눈 것이므로, 다음과 같습니다.

\[T_{\text{comms per AllGather or ReduceScatter}} = \frac{V}{W_\text{ici}}\] \[T_{\text{comms per AllReduce}} = 2 \cdot \frac{V}{W_\text{ici}}\]

여기서 \(W_\text{ici}\)는 우리가 축소할 완전한 링을 가지고 있는 한 양방향 대역폭입니다.

Case 4: 두 피연산자 모두 축소되지 않는 차원이 동일한 축을 따라 분할된 경우

각 메시 차원은 텐서를 샤딩할 때 최대 한 번만 나타날 수 있습니다. 위 규칙을 수행하다 보면 이 규칙이 위반되는 상황이 발생할 수 있습니다. 예를 들면 다음과 같습니다.

\[A[I_X, J] \cdot B[J, K_X] \rightarrow C[I_X, K_X]\]

이는 유효하지 않습니다. 왜냐하면 차원 X를 따르는 특정 샤드, 예를 들어 i는 C의 (i, i)번째 샤드, 즉 대각선 항목(diagonal entry)을 가질 것이기 때문입니다. 그러면 모든 샤드 중에서 결과의 대각선 항목 외에는 복구할 정보가 충분하지 않으므로 이 샤딩을 허용할 수 없습니다.

이를 해결하는 방법은 일부 차원을 AllGather하는 것입니다. 여기에는 두 가지 선택지가 있습니다:

\[\begin{align*} \textbf{AllGather}_X A[I_X, J] \rightarrow &\ A[I, J] \\ A[I, J] \cdot B[J, K_X] \rightarrow &\ C[I, K_X] \end{align*}\]

또는

\[\begin{align*} \textbf{AllGather}_X B[J, K_X] \rightarrow &\ B[J, K] \\ A[I_X, J] \cdot B[J, K] \rightarrow &\ C[I_X, K] \end{align*}\]

어느 경우든, 결과는 그 형태에서 X를 한 번만 언급할 것입니다. 어느 것을 선택할지는 다음 연산에 필요한 샤딩에 따라 결정됩니다.

A Deeper Dive into TPU Communication Primitives

이전의 4가지 사례는 분할된 행렬 곱셈을 수행하는 데 사용되는 몇 가지 “핵심 통신 기본 연산(core communication primitives)”을 소개했습니다:

  1. AllGather: 샤딩에서 아래 첨자(subscript)를 제거하여 샤드를 수집합니다.
  2. ReduceScatter: “축소되지 않은(un-reduced)” 접미사를 가진 배열을 해당 축에 대해 샤드를 합산하여 제거하고, 배열을 두 번째 축에 걸쳐 샤딩된 상태로 둡니다.
  3. AllReduce: “축소되지 않은(un-reduced)” 접미사를 제거하여, 해당 축에 대해 배열을 샤딩되지 않은 상태로 둡니다.

Mixture of Experts(MoE) 모델 및 기타 계산의 경우에 발생하는 또 다른 핵심 통신 기본 연산이 있습니다: AllToAll.

Our final communication primitive: the AllToAll

분할된 행렬 곱셈을 고려할 때 자연스럽게 떠오르지는 않지만 실제로는 끊임없이 나타나는, 마지막 기본 집합 연산은 AllToAll 집합 연산, 또는 더 정확하게는 샤딩된 전치(sharded transposition) 또는 리샤딩 연산의 특수한 경우입니다. 예:

\[\textbf{AllToAll}_{X, J} A[I_X, J] \rightarrow A[I, J_X]\]

AllToAll은 호환되지 않는 레이아웃 체계를 가진 분할된 계산의 다른 영역 간에 분할된 레이아웃을 재정렬하는 데 일반적으로 필요합니다. 이는 분할된 전문가 혼합 모델을 고려할 때 자연스럽게 발생합니다. AllToAll을 한 축에서 다른 축으로 아래 첨자(subscript)를 이동하는 것으로 생각할 수 있습니다. AllToAll은 각 샤드의 모든 데이터를 링 전체에 복제할 필요가 없기 때문에 실제로는 AllGather보다 저렴합니다 (¼배)짝수 크기의 양방향 링의 경우, 각 디바이스는 오른쪽으로 $(N/2 + (N/2-1) + … + 1)$개의 청크와 왼쪽으로 $((N/2-1) + … + 1)$개의 청크를 보냅니다. 이는 $= 0.5 \cdot (N / 2) \cdot (N/2 + 1) + 0.5 \cdot (N / 2) \cdot (N/2 - 1) = N^2/4$와 같습니다. 각 청크(즉, 샤드의 샤드)의 크기는 $(\text{bytes} / N^2) \cdot N^2 / 4 = \text{bytes} / 4$입니다. 이 결과는 총 대역폭이 디바이스 수에 따라 확장되므로 모든 디바이스에 걸쳐 확장됩니다..

ND AllToAll로 일반화하면, AxBxC 메시 위의 $V$ 바이트 배열에 대한 전체 비용은 다음과 같습니다.

\[T_\text{comms per AllToAll} = \frac{V \cdot \max(A, B, C, ...)}{4 \cdot N \cdot W_\text{ici}}\]

여기서 평소와 같이 $W_\text{ici}$는 양방향 ICI 대역폭입니다. 1D 메시의 경우, 이는 $V / (4 \cdot W_\text{ici})$로 줄어들며, 이는 AllReduce 비용의 1/4입니다. 2D에서는 비용이 실제로 가장 작은 축의 크기에 따라 줄어듭니다.

참고: 대략적인 유도를 원한다면, 1D 토러스 $\mathbb{Z} / N\mathbb{Z}$에서 시작하세요. 임의의 소스 노드와 타겟 노드를 선택하면 평균적으로 N / 4 홉 떨어져 있으므로 $(V \cdot N) / (4 * N)$의 비용이 듭니다. 이제 ND 토러스를 고려하면, 각 축은 기본적으로 독립적입니다. 각 노드는 $1 / N$ 바이트를 가지며 평균적으로 데이터를 $\max(A, B, C, …) / 4$ 홉만큼 이동시켜야 합니다.

More about the ReduceScatter

ReduceScatter는 보이는 것보다 더 중추적이고 근본적인 연산입니다. 왜냐하면 실제로는 AllGather의 미분(derivative)이며, 그 반대도 마찬가지이기 때문입니다. 즉, 순방향 패스에서 다음과 같다면:

\[\textbf{AllGather}_X A[I_X] \rightarrow A[I]\]

그러면 역방향 모드 미분 A’(일반적으로 각 샤드에서 다를 것임)을 ReduceScatter하여 샤딩된 A’를 도출합니다:

\[\textbf{ReduceScatter}_X A'[I] \{ U_X \} \rightarrow A'[I_X]\]

마찬가지로, 순방향 패스에서 \(\text{ReduceScatter}_X(A[I] \{U_X\}) \to A[I_X])\)는 역방향 패스에서 \(\text{AllGather}_{X}(A'[I_X]) \to A'[I]\)를 의미합니다.

AllGather와 ReduceScatter가 서로의 미분인 이유에 대한 자세한 내용은 여기를 클릭하세요.

이는 브로드캐스트와 리듀스가 선형 연산자로서 서로 전치(transpose) 관계에 있고, AllGather와 ReduceScatter가 각각 브로드캐스트와 리듀스의 외적(크로네커 곱(Kronecker products)이라고도 함)이라는 사실에서 비롯됩니다. 구체적으로, 벡터 $x \in \mathbb{R}^n$, 임의의 디바이스 수 $p \in \mathbb{N}$가 있고, $u = (1, \ldots, 1) \in \mathbb{R}^p$라고 하면, 직관적인 이해와 일치하도록 브로드캐스트와 리듀스를 다음과 같이 정의할 수 있습니다:

\[\begin{align*} \text{broadcast} &: \mathbb{R}^n \rightarrow \mathbb{R}^{p n} \\ \text{broadcast} &= u \otimes \mathbf{I}_n \\ \text{reduce} &: \mathbb{R}^{p n} \rightarrow \mathbb{R}^n \\ \text{reduce} &= u^T \otimes \mathbf{I}_n \end{align*}\]

$n = 1$, $p = 2$인 예제에서 이것이 어떻게 보이는지 확인해 봅시다. $x = (7)$이면, \(\text{broadcast}(x) = \left(\begin{pmatrix} 1 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 1 \end{pmatrix}\right) x = \begin{pmatrix} 1 \\ 1 \end{pmatrix} x = \begin{pmatrix} 7\\ 7 \end{pmatrix} \in \mathbb{R}^{p n}\)입니다. 이는 $\mathbb{R}^n$의 벡터를 $\mathbb{R}^{pn}$으로 브로드캐스팅하는 예상과 일치합니다. 이제 $y = (8, 9)$라고 하면, \(\text{reduce}(y) = \left(\begin{pmatrix} 1 & 1 \end{pmatrix} \otimes \begin{pmatrix} 1\end{pmatrix}\right) y = \begin{pmatrix} 1 & 1 \end{pmatrix} \begin{pmatrix} 8 \\ 9 \end{pmatrix} = \begin{pmatrix} 17 \end{pmatrix}\)입니다. 이 또한 $\mathbb{R}^{p n}$의 벡터를 $\mathbb{R}^{n}$의 벡터로 줄이는 예상과 일치합니다. 모든 두 행렬 $A$와 $B$에 대해 $(A \otimes B)^T = A^T \otimes B^T$이므로, $\text{reduce} = \text{broadcast}^T$임을 알 수 있습니다. 우리는 다음과 같은 외적으로 AllGather와 ReduceScatter를 복구합니다:

\[\begin{align*} \text{AllGather} &: \mathbb{R}^{p n} \rightarrow \mathbb{R}^{p^2 n} \\ \text{AllGather} &= \text{broadcast} \otimes \mathbf{I}_p \\ \text{ReduceScatter} &= \mathbb{R}^{p^2 n} \rightarrow \mathbb{R}^{p n} \\ \text{ReduceScatter} &= \text{reduce} \otimes \mathbf{I}_p \end{align*}\]

여기서 $\mathbb{R}^{p^2 n}$은 $\mathbb{R}^{p \times p n}$으로 생각하므로, $p$개의 디바이스 각각에 대해 하나의 $\mathbb{R}^{p n}$ 벡터입니다. 작은 예제, 예를 들어 $n = 2$, $p = 3$으로 행렬로서 이 연산자들이 어떻게 보이는지 확인해 보는 것을 추천합니다. 동일한 전치 속성을 사용하여, 우리는 다시 한번 $\text{AllGather}^T = \text{ReduceScatter}$를 얻고, 물론 $\text{ReduceScatter}^T = \text{AllGather}$를 얻습니다. 이 전치는 역전파 중에 발생합니다. AllGather나 ReduceScatter와 같은 선형 연산자 $A$에 대해 $y = Ax$가 있다면, 역전파 중에 $y$에 대한 손실의 미분 $\frac{\partial L}{\partial y}$가 있고, $\frac{\partial L}{\partial x} = A^T \frac{\partial L}{\partial y}$로서 $\frac{\partial L}{\partial x}$를 얻습니다. 이것은 AllGather의 미분이 ReduceScatter가 되는 방식과 그 반대의 경우를 보여줍니다.

AllReduce를 AllGather와 ReduceScatter로 바꾸는 것은 최종 AllGather를 나중의 어느 순간으로 연기(defer)할 수 있다는 편리한 속성도 가지고 있습니다. 매우 흔하게 우리는 전체 행렬 곱을 디바이스에 걸쳐 복제하여 재조립하는 비용을 지불하고 싶지 않습니다. 오히려 우리는 축소 차원이 샤딩된 두 피연산자를 결합하는 이 경우에도 샤딩된 상태를 보존하고 싶습니다:

\[A[I, J_X] \cdot B[J_X, K] \rightarrow C[I, K_X]\]

이 경우, AllReduce 대신 ReduceScatter를 수행한 다음, 선택적으로 나중에 AllGather를 수행할 수 있습니다. 즉,

\[\begin{align*} A[I, J_X] \cdot_{LOCAL} B[J_X, K] \rightarrow &\ C[I, K] \{ U_X \} \\ \textbf{ReduceScatter}_{X,K} C[I, K] \{ U_X \} \rightarrow &\ C[I, K_X] \end{align*}\]

ReduceScatter는 샤딩된 차원을 도입하므로, 이 경우 I 또는 K 이름 있는 차원을 따라 샤딩할 자연스러운 자유를 가집니다. 일반적으로 ReduceScatter를 사용할 때 새로운 샤딩을 도입할 어떤 이름 있는 차원을 선택해야 합니다(선택은 보통 더 큰 모델링 컨텍스트에 의해 강제되지만). 이것이 우리가 샤딩할 축을 지정하기 위해 ReduceScatterX,K 구문을 사용하는 이유입니다.

How to overlap matmul communication with compute

파트 1에서 논의했듯이, 통신 속도가 충분히 빠르다면 일반적으로 통신을 유용한 계산과 중첩(overlap)시킬 수 있다고 가정합니다. 이 섹션의 집합 연산들은 일반적으로 행렬 곱셈 계산 자체와 중첩될 수 있지만, 그렇게 하는 것은 간단하지 않습니다. 우리가 사용하는 알고리즘은 collective matmul이라고 하며, Wang et al.에서 처음 설명되었습니다. 다음은 이 중첩이 어떻게 구현될 수 있는지 보여주는 간소화된 애니메이션입니다:

Figure: 단일 샤딩된 행렬-벡터 곱(matrix-vector product)이 결과 AllReduce(위의 case 3)와 어떻게 중첩될 수 있는지 보여주는 애니메이션. 전체 matmul은 여러 행렬-벡터 곱으로 구성됩니다.

간단히 말해, 이전 청크에 대한 링 축소(ring reduction)를 시작하면서 행렬의 한 청크에 대한 matmul을 수행할 수 있습니다. 어떤 경우에는 배치 차원이나 행렬 입력 차원에 대해 타일링(tile)할 수도 있습니다. 파트 10에서 간단한 JAX 구현을 다루고, Mosaic 문서에서도 GPU에 대한 좋은 예제를 제공합니다. 언젠가 이것의 버전을 직접 구현해 보는 것을 권장합니다.

What Have We Learned?

\[T_{\text{comm per AllGather or ReduceScatter}} = \frac{\text{Data volume}}{\text{bandwidth}} \cdot \frac{\text{Axis} - 1}{\text{Axis}} \longrightarrow \frac{\text{Data volume}}{\text{bandwidth (bidirectional)}}\]
Operation Description Syntax Runtime
AllGather Gathers all the shards of a sharded array along an axis, removing a subscript. $[A_X, B] \to [A, B]$ bytes / (bidirectional ICI bandwidth * num_axes)
ReduceScatter Sums a partially summed array along an axis and shards it along another axis (adding a subscript). $[A, B] \{U_X\} \to [A_X, B]$ Same as AllGather
AllReduce Sums a partially summed array along an axis. Removes a { Ux }. Combines an AllGather and ReduceScatter. $[A_X, B]\{U_Y\} \to [A_X, B]$ 2 * AllGather
AllToAll Gathers (replicates) an axis and shards a different dimension along the same axis. $[A, B_X] \to [A_X, B]$ AllGather / 4 for a bidirectional ring

Some Problems to Work

이 섹션의 내용을 바탕으로 한 몇 가지 유익한 문제입니다. 현재 모든 답을 포함하고 있지는 않지만, 가능한 한 더 많은 답을 작성해 나갈 예정입니다.

Question 1 [replicated sharding]: 배열이 $A[I_X, J, K, \ldots]$로 샤딩되어 있고(즉, $X$에 대해서만 샤딩됨), 메시가 Mesh({'X': 4, 'Y': 8, 'Z': 2})라고 합시다. 모든 칩에 걸쳐 $A$가 차지하는 총 바이트 수와 배열의 단일 사본 크기의 비율은 얼마인가요?

답을 보려면 여기를 클릭하세요.

배열은 크기가 4인 X를 따라서만 샤딩되므로, 각 샤드의 크기는 $[I / 4, J, K, \ldots] = \text{sizeof}(A) / 4$입니다. 배열이 Y와 Z에 걸쳐 복제되므로 총 크기는 $Y \cdot Z \cdot \text{sizeof}(A)$이며, 따라서 총 크기 대 단일 칩 크기의 비율은 $Y \cdot Z \cdot \text{sizeof}(A) / \text{sizeof}(A) = 16$입니다.

Question 2 [AllGather latency]: $B=1024$, $D=4096$이고 bfloat16을 사용할 때, 메시 Mesh({'X': 4, 'Y': 4, 'Z': 4})를 가진 TPUv4p 4x4x4 슬라이스에서 $\text{AllGather}_X([B_X, D_Y])$는 얼마나 걸릴까요? \(\text{AllGather}_{XY}([B_X, D_Y])\)는 어떨까요? \(\text{AllReduce}_Z([B_X, D_Y] \{U_Z \})\)는 어떨까요?

답을 보려면 여기를 클릭하세요.

완전한 4x4x4 큐브를 가지고 있으므로 모든 축에 랩어라운드 링크가 있어 9e10 양방향 대역폭을 사용할 수 있습니다.

  1. 하나의 축에 대해서만 gather를 수행하고 다른 축은 샤딩되어 있으므로, 1개의 축에 대해 $2BD / Y$ 바이트를 효과적으로 gather하는 셈입니다. Y축을 따른 단일 샤드만 생각해보면, X를 따른 AllGather는 1 / Y 바이트를 가진 샤딩되지 않은 AllGather처럼 보입니다. TPU v4p의 양방향 ICI 대역폭이 9e10 bytes/second이므로, 이 작업은 $2BD / (\text{9e10} \cdot Y) = 2 \cdot 1024 \cdot 4096 / (\text{9e10} \cdot 4) = 23 \mu s$가 걸립니다.

  2. 이전보다 대역폭이 두 배이지만 전체 배열을 AllGather하고 있으므로, T = 2BD / (2 * W) = 2*1024*4096 / (2 * 9e10) = 46us입니다. 이는 지연 시간 한계인 4us(홉당 1us)보다 훨씬 크므로 괜찮습니다.

  3. AllReduce의 비용은 AllGather의 두 배입니다. 각 샤드의 크기는 $2BD / (X * Y)$이므로, 비용은 약 $4BD / (X * Y * W)$, 또는 대략 4 * 1024 * 4096 / (16 * 9e10) = 11.6us입니다.

Question 3 [latency-bound AllGather]: $\text{AllGather}_X([B_X])$를 수행한다고 가정해 봅시다. 하지만 $B$가 매우 작습니다(예: 128). bfloat16에서 메시 Mesh({'X': 4, 'Y': 4, 'Z': 4})를 가진 TPUv4p 4x4x4 슬라이스에서 이 작업은 얼마나 걸릴까요? 힌트: 아마도 latency bound일 것입니다.

답을 보려면 여기를 클릭하세요.

bfloat16에서 배열은 총 256 바이트만 사용하며, 디바이스당 64 바이트입니다. TPU v4p에서 크기 4인 축을 가지고 있으므로 랩어라운드 링크가 있어 양방향으로 배열을 보낼 수 있습니다. 4.5e10의 단방향 대역폭으로 각 홉은 대략 64 / 4.5e10 ~ 0이 걸리므로 확실히 latency bound입니다. 홉 수를 세어보면 단 2홉 만에 전체 gather를 수행할 수 있으므로, 대략 2us가 좋은 추정치입니다.

Question 4 [matmul strategies]: $X[B, D] \cdot_D Y[D_X, F] \to Z[B, F]$를 수행하기 위해, 이 섹션에서는 $\text{AllGather}_X(Y[D_X, F])$를 수행하고 완전히 복제된 행렬을 곱하라고 설명합니다(Case 2, 전략 1). 대신, $X[B, D_X] \cdot_D Y[D_X, F] \to Z[B, F] \{U_X\}$와 같이 로컬 샤드를 곱하고(Case 4, 전략 2), 그 다음 $\text{AllReduce}_X(Z[B, F] \{ U_X\})$를 수행할 수도 있습니다. 각각 얼마나 많은 FLOPs와 통신을 수행하나요? 어느 것이 더 낫고 그 이유는 무엇인가요?

답을 보려면 여기를 클릭하세요.

기본 전략(전략 1)부터 시작해 봅시다. 앞서 보았듯이 AllGather 비용은 $2DF / W_\text{ici}$입니다. 완전히 복제된 배열을 얻으면 총 계산 시간은 $2BDF / C$입니다(여기서 $C$는 가속기 FLOPs/s이며, 각 TPU가 동일한 FLOPs를 수행합니다). 따라서 우리는 다음과 같습니다:

\[T_\text{total (Strategy 1)} = \max\left(\frac{2BDF}{C}, \frac{2DF}{W_\text{ici}}\right)\]

이에 비해, 새로운 전략(전략 2)은 $2BF$ 바이트에 대해 AllReduce를 수행하며, 비용은 $4BF / W_\text{ici}$이지만 FLOPs는 $1 / X$ 적게 수행합니다(계산이 샤딩되므로). 즉, $2\cdot B\cdot D\cdot F / X$ FLOPs를 수행하고 결과 AllReduce는 bfloat16에서 \(2 \cdot 2 \cdot B \cdot F\) 바이트를 통신합니다. 따라서, 전략 2(AllGather 없음, 나중에 AllReduce만 있음)의 총 시간은 대략 다음과 같습니다:

\[T_\text{total} = \max\left(\frac{2BDF}{X \cdot C}, \frac{4BF}{W_\text{ici}}\right)\]

질문은: 이 중 어느 것이 더 큰가요? 전략 (2)는 $D / (X \cdot C) > 2 / W_\text{ici}$일 때, 또는 $D / 2X > C / W_\text{ici} \approx 2550 \rightarrow X < D / (2 * 2550)$일 때 compute bound입니다. 합리적으로 $D \approx 8k$라고 예상할 수 있으므로, 이는 대략 $X < 2$를 의미하며 이는 가능성이 낮습니다. 따라서 전략 2에서는 기본적으로 항상 comms bound입니다. 기본 전략(전략 1)에서는 \(B < C / W_\text{ici} = 2550\)일 때 comms bound이며, 이는 자주는 아니지만 종종 사실입니다.

따라서 $B < 2550$이면 두 경우 모두 comms-bound이며, 다음이 성립합니다:

\[T_\text{comms for Strategy 2} < T_\text{comms for Strategy 1} \Leftrightarrow \frac{4BF}{W_\text{ici}} < \frac{2DF}{W_\text{ici}}\]

이는 $D > 2B$일 때 참이며, 여기서 $2B < 5100$입니다. 이는 종종 사실이므로, 배치가 작다면 전략 2가 때때로 더 나을 수 있습니다. 배치가 클 때($B > 2550$)는 다음과 같습니다:

\[T_\text{comms for Strategy 2} < T_\text{math for Strategy 1} \Leftrightarrow \frac{4BF}{W_\text{ici}} < \frac{2BDF}{C}\]

이는 $2 / W_\text{ici} < D / C$일 때, 또는 $D > 2 * 2550 = 5100$일 때 참이며, 대규모 모델에서는 보통 사실입니다. 따라서 이 대안 전략은 $D$가 작지 않은 한 일반적으로 대규모 모델에 더 좋습니다.

왜 항상 이렇게 하지 않을까요? 실제로는 가끔 이렇게 할 수도 있지만, matmul 입력 중 하나의 축소 차원이 다른 입력이 샤딩되지 않은 축을 따라 샤딩되는 경우는 드뭅니다. 예를 들어, FSDP(섹션 5에서 설명)를 수행하는 경우 파라미터를 데이터 차원에 걸쳐 샤딩하지만, 활성화도 데이터를 따라 샤딩됩니다. 그런 의미에서 이런 경우는 잘 나타나지 않습니다.

Question 5 [minimum latency]: 가장 낮은 지연 시간으로 TPUv5p 4x4x4에서 matmul $A[I, J] \cdot_J B[J, K] \to C[I, K]$를 수행하고 싶다고 가정해 봅시다. 입력은 임의로 샤딩될 수 있지만 결과는 완전히 복제되어야 한다고 가정합니다. 입력을 어떻게 샤딩해야 할까요? 총 FLOPs와 통신 시간은 얼마인가요?

답을 보려면 여기를 클릭하세요.

여기서 전체 답변을 제공하지는 않겠지만, 가장 가능성 높은 네 가지 옵션을 설명하는 것으로 시작하겠습니다:

  1. $A[I_{XYZ}, J] \cdot B[J, K]$ + 끝에 AG
  2. $A[I, J] \cdot B[J, K_{XYZ}]$ + 끝에 AG
  3. $A[I, J_{XYZ}] \cdot B[J_{XYZ}, K]$ + 끝에 AR
  4. $A[I, J] \cdot B[J, K]$ (완전 복제)

다른 축을 다른 메시 축을 따라 샤딩하는 것도 고려할 수 있지만, 최종 비용은 변경되지 않을 가능성이 높습니다. (4)를 제외한 모든 경우에 대해 TPU당 총 FLOPs는 동일하지만 통신은 각각 다릅니다. 그런 다음 각 비용에 대한 통신 비용을 계산하고 어느 것이 가장 낮은지 확인하면 됩니다. 요약하자면 (1)과 (2)가 똑같이 좋습니다.

Question 6: TPUv5e 4x4에서 $A[I_X, J_Y] \cdot_J B[J_Y, K] \to C[I_X, K]$를 수행하고 싶다고 가정해 봅시다. 어떤 통신을 수행해야 할까요? 통신 대 계산에 소요되는 시간은 얼마인가요?

Question 7: 일반적인 트랜스포머 블록에는 $F \gg D$인 두 행렬 $W_\text{in}[D, F]$와 $W_\text{out}[F, D]$가 있습니다. 배치 크기 B가 있다고 합시다. 그러면 전체 블록은 $In[B, D] \cdot W_\text{in}[D, F]. \cdot W_\text{out}[F, D]$입니다. $D=8192$, $F=32768$, $B=128$로 정하고 모든 것이 bfloat16이라고 가정합시다. TPUv5e 2x2 슬라이스에서 실행하고 있지만 각 TPU에 300MB의 여유 메모리만 있다고 가정해 봅시다. In, $W_\text{in}$, $W_\text{out}$, Out을 어떻게 샤딩해야 메모리 제한 아래에 머물면서 전체 시간을 최소화할 수 있을까요? 통신과 FLOPs에 얼마나 많은 시간이 소요되나요? 힌트: 최종 출력은 완전히 복제될 필요는 없지만, “레이어”가 반복될 수 있도록 입력과 동일하게 샤딩되어야 합니다.

답을 보려면 여기를 클릭하세요.

먼저 메모리에 대해 생각해 봅시다. 두 개의 큰 행렬은 각각 2 * 8192 * 32768 = 536MB를 사용합니다. 활성화 In의 크기는 128 * 8192 = 1MB입니다(걱정할 필요 없을 만큼 작음). 각 디바이스에 300MB의 여유 메모리만 있으므로 matmul을 샤딩해야 합니다.

  1. $In[B_X, D] * W_\text{in}[D_{XY}, F] * W_\text{out}[F, D_{XY}] \rightarrow Out[B, D]$ (이를 흔히 FSDP라고 함)
  2. $In[B, D_{XY}] * W_\text{in}[D, F_{XY}] * W_\text{out}[F_{XY}, D] \rightarrow Out[B, D_{XY}]$ (이를 텐서 병렬 처리라고 함)

첫 번째는 큰 가중치나 활성화를 먼저 AllGather해야 하기 때문에 꽤 나쁩니다. 두 번째는 처음에 AllGather가 필요하고 끝에 ReduceScatter가 필요합니다(AllReduce보다 저렴함). 나머지 수학 계산은 연습으로 남겨두겠습니다.

Question 8 [challenge]: 위의 짧은 코드 스니펫을 템플릿으로 사용하여, 샤딩된 배열을 할당하고 pmap 또는 shard_map을 사용하여 4가지 주요 통신 기본 연산(AllGather, AllReduce, ReduceScatter, AllToAll) 각각을 벤치마킹하세요. jax.lax.all_gather, jax.lax.psum, jax.lax.psum_scatter, jax.lax.all_to_all을 사용해야 할 것입니다. 이 함수들의 의미를 이해하시나요? 얼마나 걸리나요?

Question 9 [another strategy for sharded matmuls?]: 위에서 우리는 matmul에 대한 입력 중 하나만 축소 차원을 따라 샤딩된 경우, 샤딩된 행렬을 AllGather하고 결과적인 축소를 로컬에서 수행해야 한다고 주장했습니다. 생각할 수 있는 또 다른 전략은 샤딩된 matmul을 수행한 다음 결과를 AllReduce하는 것입니다(마치 두 입력이 모두 축소 차원을 따라 샤딩된 것처럼). 즉, $A[I, J_X] *_J B[J, K] \to C[I, K]$를 다음과 같이 수행합니다.

  1. $C[I, K] \{ U_X \} = A[I, J_X] \cdot B[J_X, K]$
  2. $C[I, K] = \text{AllReduce}(C[I, K] \{ U_X\})$

다음에 답하세요:

  1. 행렬 $A[N, M]$과 $B[M, K]$에 대해 이 알고리즘을 명시적으로 작성하고, 인덱스를 사용하여 어떤 디바이스에서 정확히 어떤 계산이 수행되는지 보여주세요. $A$는 ND 디바이스에 걸쳐 $A[I, J_X]$로 샤딩되어 있다고 가정하고, 출력이 모든 디바이스에 걸쳐 복제되기를 원한다고 가정합니다.
  2. 이제 최종 결과가 각 디바이스에 복제되는 대신 샤딩되는 것(N 또는 K 차원에 걸쳐)으로 충분하다고 가정해 봅시다. 위의 알고리즘은 어떻게 변할까요?
  3. 위의 전략( (a)가 아닌 (b)의 경우)의 통신 비용만 볼 때, 이 통신 비용은 A를 먼저 AllGather한 다음 matmul을 수행하는 알고리즘의 통신 비용과 어떻게 비교되나요?
답을 보려면 여기를 클릭하세요.
  1. 먼저 외적을 계산하여 결과를 \(O[N, K]: o_{kj} = \sum_i a_{ki} b_{ij}\)에 저장합니다. 외적을 수행하고 있으므로 반복되는 인덱스는 축소되는 인덱스가 아닙니다. 여기서 합계는 사용 중인 특정 디바이스에 저장된 i 값의 범위를 나타냅니다. 예를 들어, 크기 16의 축소 축과 4개의 디바이스가 있다면, 디바이스 0에서 i는 {0, 1, 2, 3} 범위이고, 디바이스 1에서 i는 {4, 5, 6, 7} 범위이며, 디바이스 2에서 i는 {8, 9, 10, 11} 범위이고, 디바이스 3에서 i는 {12, 13, 14, 15} 범위입니다. 그런 다음 각 디바이스에 있는 $O[N, K]$의 부분 합을 AllReduce하여 전체 $O[N, K]$를 형성합니다.
  2. 2단계에서 AllReduce를 수행하는 대신, 어느 축을 따라서든 더 저렴한 ReduceScatter로 해결할 수 있습니다: $[N, K] \{ U_X \} \to [N_X, K]$ 또는 $[N, K] \{ U_X \} \to [N, K_X]$.
  3. 본문에서 설명한 대로, AllGather를 수행하는 비용(throughput-bound일 때)은 ReduceScatter의 비용과 동일합니다. 이는 단순히 우리가 처리하는 전체 행렬의 크기로 주어집니다. 따라서 gather-then-matmul 알고리즘에서 이는 $NM$으로 확장됩니다($A$를 $\text{AllGather}$하고 있으므로). matmul-then-reduce-scatter 알고리즘에서 이는 NK로 확장됩니다($O$를 reduce-scattering하고 있으므로). 따라서 두 알고리즘의 통신 비용 비율은 M/K입니다.

Question 10: Fun with AllToAll: 위의 표에서, AllToAll을 수행하는 시간은 AllGather 또는 ReduceScatter를 수행하는 시간보다 4배 더 낮다고 언급되었습니다(throughput-bound인 경우). 이 문제에서는 그 4배라는 요소가 어디서 오는지 살펴보고, 양방향 ICI 링크가 아닌 단방향 ICI 링크만 있는 경우 이 요소가 어떻게 변하는지 살펴볼 것입니다.

  1. 먼저 단방향의 경우부터 시작해 봅시다. 링 토폴로지에 D개의 디바이스가 있고, $A[I_X, J]$로 샤딩된 N x N 행렬 A에 대해 AllGather 또는 ReduceScatter를 수행한다고 가정해 봅시다(단순화를 위해 $D$가 $N$을 나눈다고 가정). 이 두 집합 연산에 포함된 통신을 설명하고, 이 알고리즘 전체 동안 단일 ICI 링크를 통해 전송되는 스칼라(실수 또는 정수)의 총 수를 계산하세요.
  2. 이제 여전히 단방향 ICI 경우에서 AllToAll에 대해 생각해 봅시다. 이 경우 알고리즘은 all-gather 경우와 어떻게 다를까요? 이 알고리즘에서 단일 ICI 링크를 통해 전송되는 스칼라의 수를 계산하세요.
  3. (a) 부분과 (b) 부분에 대한 답의 비율이 좋은 숫자가 됨을 발견했을 것입니다. 이 요소가 어디서 오는지 간단한 용어로 설명하세요.
  4. 이제 양방향 통신을 추가해 봅시다. 이것이 all-gather 경우에 필요한 총 시간에 어떤 영향을 미치나요?
  5. 양방향 통신을 추가하는 것이 AllToAll 경우에 필요한 총 시간에 어떤 영향을 미치나요?
  6. 이제 양방향 링에서 AllGather 시간과 AllToAll 시간 사이의 비율을 설명하세요.
답을 보려면 여기를 클릭하세요.

(1) Solution: 과정은 간단합니다. 알고리즘의 각 단계에서 각 디바이스는 행렬의 단일 샤드 “스트립(strip)”(총 \(\frac{N}{D} \times N\)크기의 요소)을 가장 가까운 이웃에게 보냅니다. 이는\(D-1\)번 발생합니다. 각 샤드는 시작한 디바이스를 제외한 모든 디바이스에 통신되어야 하기 때문입니다. 따라서 총 \(\frac{N^2(D-1)}{D}\) 스칼라가 각 디바이스에 의해 전송됩니다. 즉, 단일 ICI 링크를 통해 흐릅니다.

Answer: \(N^2 (1-\frac{1}{D})\), 또는 \(D >> 1\)일 때 단순히 \(N^2\).

(2) Solution: 통신 관점에서 AllToAll과 AllGather의 주요 차이점은 AllToAll의 경우 특정 디바이스에 있는 샤드 전체를 다른 모든 디바이스에 통신할 필요가 없다는 것입니다. 특정 디바이스(디바이스 0이라고 함)에 저장된 샤드가 \([A, B, C, D]\)라고 상상해 봅시다(여기서 A, B, C, D는 행렬이며 설명을 위해 4개의 디바이스가 있는 링을 상상합니다). 이제 행렬 \(A\)는 어디에도 통신될 필요가 없고, 행렬 \(B\)는 디바이스 1에, 행렬 \(C\)는 디바이스 2에, 행렬 \(D\)는 디바이스 3에 도달해야 합니다. 따라서 알고리즘의 첫 번째 단계에서 우리는 \(B\), \(C\), \(D\)를 디바이스 1로 보냅니다. 다음 단계에서 디바이스 1은 \(C\)와 \(D\)를 디바이스 2로 보냅니다. 마지막 단계에서 디바이스 2는 \(D\)만 디바이스 3으로 보냅니다. 이 경우 전송되는 파라미터의 총 수는 \((\text{size of A/B/C/D}) * (3 + 2 + 1)\)입니다. A/B/C/D의 크기는 (이제 일반적인 경우에서) \(\frac{N^2}{D^2}\)이고, 다시 일반적인 경우에서 \((3 + 2 + 1)\)항은\(((D-1) + (D-2) + … + 1)\), 또는 \(\frac{(D)(D-1)}{2}\)가 됩니다. 따라서 단일 ICI 링크를 통해 전송되는 총 바이트 수는 \(\frac{N^2(D-1)}{D \times 2}\)입니다.

Answer: \(\frac{N^2}{2}(1-\frac{1}{D})\), 또는 \(D >> 1\)일 때 단순히 \(\frac{N^2}{2}\).

(3) Solution: 비율은 단순히 \(\frac{1}{2}\)입니다. 즉, 단방향 링 토폴로지에서 AllToAll은 all-gather/ReduceScatter보다 비용이 절반입니다. 위의 유도를 살펴보면, 이는 궁극적으로 all-gather 경우에 매번 \((D-1)\)번 동일한 크기의 블록을 전송하고 있다는 사실, 즉 합계 \(\text{tiny block size} * (D + D + D + … + D)\)를 수행하는 반면, AllToAll의 경우 합계\(\text{tiny block size} * (D + D-1 + D-2 + … + 1)\)를 수행하고 있다는 사실에서 비롯됩니다. 따라서 2라는 요소는 본질적으로 \(1 + 2 + \ldots + n = n(n+1)/2\)라는 사실에서 나옵니다.

(4) Solution: 어떤 링크 하나가 운반해야 하는 총 스칼라 수는 2배로 줄어듭니다. 양방향 링에서는 각 “샤딩된 스트립”을 동시에 두 방향으로 보낼 수 있기 때문입니다.

(5) Solution: 이 경우 단방향 경우에 비해 4배의 이득을 얻습니다. 이는 단일 샤딩된 스트립(디바이스 0에서 시작된 것)에 있는 각 크기-(N2/D2) 블록의 운명을 고려하면 가장 쉽게 알 수 있습니다. (단방향 경우처럼) 이 블록 중 하나를 거리 D-1, 다른 블록을 거리 D-2 등으로 1까지 보내는 대신, 이제 스트립을 오른쪽이나 왼쪽으로 이동하는 블록으로 나누어 최대 거리 floor(D/2)만큼 이동합니다. 따라서 해당 합계는 이제 \(D/2 + D/2 - 1 + D/2 - 2 + … = D/2 \cdot (D/2+1)/2\), 또는 큰 \(D\)한계에서\(D^2/8\)이 됩니다. 이를 단방향 경우의 \(D^2/2\)와 비교하면 4배의 이득을 얻었음을 알 수 있습니다.

(6) Solution: 단방향 링에서 AllToAll 시간은 all-gather 시간보다 이미 두 배 빠르다는 것을 보았습니다. 이는 전체 스트립을 모든 단일 디바이스에 보낼 필요가 없다는 사실에서 비롯됩니다. 그런 다음 양방향성을 추가했을 때, AllToAll에는 4배의 이득이 있었고 all-gather에는 2배의 이득만 있었다는 것을 보았습니다. 이 비율들을 합치면 우리가 찾던 4라는 요소를 얻게 됩니다.

파트 3은 여기까지입니다! 파트 4(트랜스포머 수학에 관한 내용)를 보려면, 여기를 클릭하세요!

Miscellaneous

*Work done at Google DeepMind, now at MatX.

Citation

For attribution in academic contexts, please cite this work as:

    Austin et al., "How to Scale Your Model", Google DeepMind, online, 2025.

or as a BibTeX entry:

    @article{scaling-book,
      title = {How to Scale Your Model},
      author = {Austin, Jacob and Douglas, Sholto and Frostig, Roy and Levskaya, Anselm and Chen, Charlie and Vikram, Sharad
      and Lebron, Federico and Choy, Peter and Ramasesh, Vinay and Webson, Albert and Pope, Reiner},
      publisher = {Google DeepMind},
      howpublished = {Online},
      note = {Retrieved from https://jax-ml.github.io/scaling-book/},
      year = {2025}
    }