All the Transformer Math You Need to Know

Part 4 of How To Scale Your Model (Part 3: Sharding | Part 5: Training)

여기서는 Transformer 아키텍처에 대해 간략히 복습하고, 구체적으로 FLOPs, bytes 및 기타 주요 수치들을 계산하는 방법을 살펴보겠습니다.

번역 안내: 원저자(Jacob Austin)의 허락을 받아 원문을 번역 중입니다.
해당 글의 1인칭은 원문 저자를 지칭합니다.
원문: How to Scale Your Model
번역: 신종훈

Counting Dots

다음과 같은 형태의 벡터 $x$,$y$와 행렬 $A$,$B$로 시작하겠습니다:

\[\def \red#1{\textcolor{red}{#1}} \def \green#1{\textcolor{green}{#1}} \def \blue#1{\textcolor{blue}{#1}} \def \purple#1{\textcolor{purple}{#1}} \def \orange#1{\textcolor{orange}{#1}} \def \gray#1{\textcolor{gray}{#1}} \begin{array}{cc} \textrm{array} & \textrm{shape} \\ \hline x & \textrm{[P]} \\ y & \textrm{[P]} \\ A & \textrm{[N P]} \\ B & \textrm{[P M]} \\ \hline \end {array}\]

이 $x \cdot y$의 내적(dot product)은 $P$개의 덧셈_과 _곱셈, 즉 총 $2P$개의 부동소수점 연산(FLOPs)을 필요로 합니다.
행렬-벡터 곱 $Ax$는 $A$의 행을 따라 $N$개의 내적을 수행하므로 $2NP$ FLOPs가 필요합니다.
행렬-행렬 곱 $AB$는 $B$의 각 열에 대해 $M$개의 행렬-벡터 곱을 수행하므로 총 $2NPM$ FLOPs가 필요합니다.
일반적으로, 일부 차원이 축약(CONTRACTING)되고 일부는 배치(BATCHING)되는 고차원 배열 $C$와 $D$가 있다면(예: $C[\blue{GH}IJ\red{KL}], D[\blue{GH}MN\red{KL}]$), 이 축약의 FLOPs 비용은 배치 및 축약 차원을 한 번만 계산한 모든 $C$와 $D$차원의 곱에 2를 곱한 값입니다(예:$2\blue{GH}IJMN\red{KL}$). 한 차원이 배치되려면 두 피연산자 모두에 나타나야 합니다. (또한, 축약 차원이 없고 이것이 단지 원소별 곱셈일 경우에는 2의 계수가 적용되지 않습니다.)

\[\begin{array}{ccc} \textrm{Operation} & \textrm{FLOPs} & \textrm{Data} \\ \hline x \cdot y & 2P & 2P \\ A x & 2NP & NP + P \\ AB & 2NPM & NP + PM \\ [c_0,...,c_N] \cdot [d_0,...,d_N] & 2 \prod c_i \times \prod_{\substack{d_j \notin \blue{BATCH} \\ d_j \notin \red{CONTRACT}}} d_j & \prod c_i + \prod d_j \\ \hline \end {array}\]

행렬-행렬 곱셈의 경우, 연산량은 3차 ($O(N^3)$)로 확장되는 반면 데이터 전송은 2차 ($O(N^2)$)로만 확장된다는 사실에 주목하세요. 이는 행렬 곱셈의 크기를 키울수록 연산 포화(compute-saturated) 한계에 도달하기가 더 쉬워진다는 것을 의미합니다. 이는 매우 이례적인 현상이며, 우리가 행렬 곱셈이 지배적인 아키텍처를 사용하는 이유를 상당 부분 설명해 줍니다. 즉, 확장에 용이하기 때문입니다!

Forward and reverse FLOPs

훈련 중에는 주어진 행렬 곱셈의 결과 자체에는 특별히 신경 쓰지 않고, 그 미분값에 더 관심이 있습니다. 이는 역전파(backpropagation) 중에 훨씬 더 많은 FLOPs를 수행한다는 것을 의미합니다.

B가 더 큰 네트워크의 한 행렬이고 A가 입력 활성화(input activations)이며 C = A B라고 상상해 봅시다. 손실(loss) L의 B에 대한 미분은 연쇄 법칙에 의해 다음과 같이 주어집니다:

\[\frac{\partial L}{\partial B} = \frac{\partial L}{\partial C}\frac{\partial C}{\partial B} = A^T \left(\frac{\partial L}{\partial C}\right)\]

이는 외적(outer product)이며, ($N$ 차원에 대해 축약되므로) 계산하는 데 $2NPM$ FLOPs가 필요합니다. 마찬가지로, 손실의 A에 대한 미분은

\[\frac{\partial L}{\partial A} = \frac{\partial L}{\partial C}\frac{\partial C}{\partial A} = \left(\frac{\partial L}{\partial C}\right) B^T\]

이며, dL/dC가 $[N, M]$ 크기의 (코)벡터이므로 다시 $2NPM$ FLOPs입니다. 이 양은 파라미터에 대한 미분은 아니지만, 네트워크의 이전 레이어에 대한 미분을 계산하는 데 사용됩니다(예: 위에서 dL/dC가 dL/dB를 계산하는 데 사용된 것처럼).

이를 모두 더하면, 훈련 중에는 총 6NPM FLOPs가 필요하며, 이는 추론 중의 2NPM에 비해 많습니다: 순방향 패스에서 2NPM, 역방향 패스에서 4NPM. PM이 행렬의 파라미터 수이므로, 이것이 훈련 중 Transformer FLOPs에 대한 유명한 $6 * \text{num parameters} * \text{num tokens}$ 근사치의 가장 간단한 형태입니다: 각 토큰은 $6 * \text{num parameters}$ FLOPs를 필요로 합니다. 아래에서 더 정확한 유도를 보여드리겠습니다.

Transformer Accounting

Transformers는 미래입니다. 음, 적어도 현재는 그렇습니다. 몇 년 전만 해도 여러 아키텍처 중 하나였을지도 모릅니다. 하지만 오늘날에는 아키텍처의 거의 모든 세부 사항을 아는 것이 가치가 있습니다. 아키텍처를 다시 소개하지는 않겠지만, 이 블로그와 원본 Transformer 논문이 도움이 되는 참고 자료가 될 수 있습니다.

다음은 Transformer 디코더 아키텍처의 기본 다이어그램입니다:

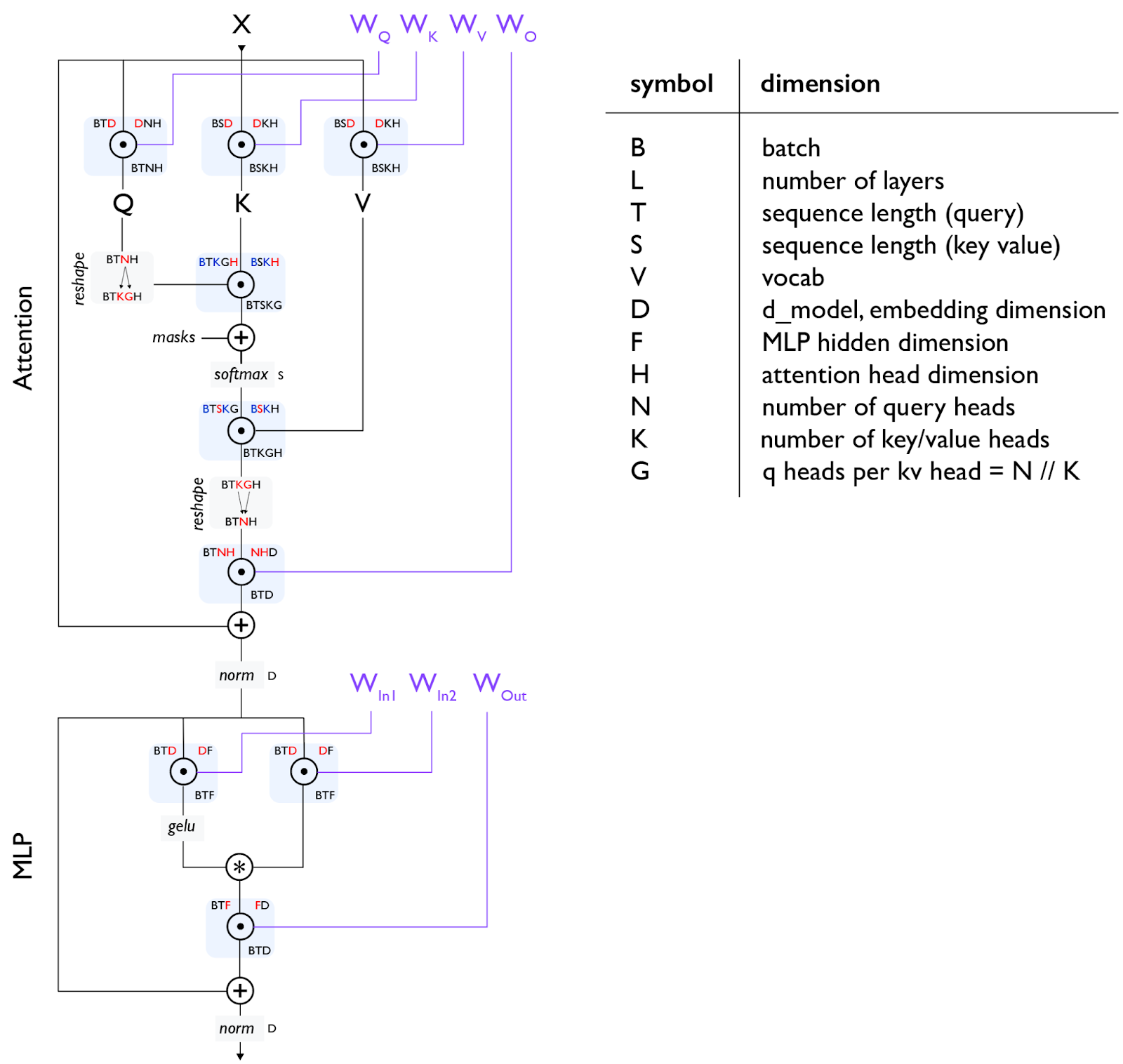
**Figure:** 이 다이어그램은 표준 트랜스포머의 한 레이어를 보여주며 위에서 아래로 흐릅니다. 트랜스포머의 배열 모양과 레이아웃을 설명하기 위해 단일 문자 규칙을 사용하며, 여기서도 축약 차원은 빨간색으로, 배치 차원은 파란색으로 표시합니다. 주어진 연산에서 입력 형태는 왼쪽 상단에, 파라미터 형태는 오른쪽 상단에 주어지며, 결과 형태는 아래에 있습니다. 예를 들어 BTD는 gating einsum의 입력 형태이고 DF는 가중치 형태입니다.

Note [gating einsum]: 위 다이어그램은 “gating einsums”을 사용합니다. 여기서는 up-projection 행렬을 두 개의 행렬($W_\text{In1}$ 및 $W_\text{In2}$)로 나누고, 그 출력들을 일종의 “게이팅 함수(gating function)”로서 원소별로 곱합니다. 모든 LLM이 이것을 사용하는 것은 아니므로, 때때로 단일 $W_\text{In}$ 행렬을 보고 총 MLP 파라미터 수가 3DF 대신 2DF인 경우를 볼 수 있습니다. 일반적으로 이 경우, 파라미터 수를 3 행렬 경우와 동일하게 유지하기 위해 D와 F를 확장합니다. 그렇긴 하지만, LLAMA, DeepSeek 및 기타 많은 모델에서 어떤 형태의 gating einsum이 사용됩니다.

Note 2 [MHA attention]: Self-attention의 경우 T와 S가 동일하지만, cross-attention의 경우 다를 수 있습니다. 바닐라 Multi-Head Attention (MHA)의 경우 N과 K가 동일한 반면, Multi-Query Attention (MQA)의 경우 K=1이고, Grouped MQA (GMQA)의 경우 K가 N을 나누기만 하면 됩니다.

Global FLOPs and Params Calculation

아래에서는 모든 곳에 L 요소를 붙이는 것을 피하기 위해 레이어당 FLOPs를 계산하겠습니다.

MLPs

Transformer의 MLP는 일반적으로 원소별로 결합되는 2개의 입력 matmul과 단일 출력 matmul로 구성됩니다:

\[\begin{array}{ccc} \textrm{operation} & \textrm{train FLOPs} & \textrm{params} \\ \hline \\ A[B,T,\red{D}] \cdot W_{in1}[\red{D}, F] & 6BTDF & DF \\[10pt] A[B,T,\red{D}] \cdot W_{in2}[\red{D}, F] & 6BTDF & DF \\[10pt] \sigma\left(A_{in1}\right)[B,T, F] * A_{in2}[B,T, F] & \gray{O(BTF)} \\[10pt] A[B,T,\red{F}] \cdot W_{out}[\red{F}, D] & 6BTDF & DF \\[10pt] \hline \\ & \approx 18BTDF & 3DF \end{array}\]

Attention

서로 다른 Q 및 KV 헤드 수를 가진 일반적인 grouped-query attention의 경우, Q,K,V projection에 대해 동일한 헤드 차원 H를 가정하고 QKVO matmul의 비용을 추정해 보겠습니다:

\[\begin{array}{ccc} \textrm{operation} & \textrm{train FLOPs} & \textrm{params} \\ \hline \\ A[B,T,\red{D}] \cdot W_{Q}[\red{D}, N, H] & 6BTDNH & DNH \\[10pt] A[B,T,\red{D}] \cdot W_{K}[\red{D}, K, H] & 6BTDKH & DKH \\[10pt] A[B,T,\red{D}] \cdot W_{V}[\red{D}, K, H] & 6BTDKH & DKH \\[10pt] A[B,T,\red{N}, \red{H}] \cdot W_{O}[\red{N}, \red{H}, D] & 6BTDNH & DNH \\[10pt] \hline \\ & 12BTD(N+K)H & 2D(N+K)H \end{array}\]

내적 어텐션 연산은 더 미묘합니다. 사실상 $B$, $K$차원에 배치된$TH \cdot HS$matmul, softmax, 그리고 다시$B$, $K$차원에 배치된$TS \cdot SH$ matmul입니다. 배치된 차원을 파란색으로 강조합니다:

\[\begin{array}{cc} \textrm{operation} & \textrm{train FLOPs} \\ \hline \\[3pt] Q[\blue{B}, T, \blue{K}, G, \red{H}] \cdot K[\blue{B}, S, \blue{K}, \red{H}] & 6BTSKGH = 6BTSNH \\[3pt] \textrm{softmax}_S \;\; L[B, T, S, K, G] & \gray{O(BTSKG) = O(BTSN)} \\[3pt] S[\blue{B}, T, \red{S}, \blue{K}, G] \cdot V[\blue{B}, \red{S}, \blue{K}, H] & 6BTSKGH = 6BTSNH \\[3pt] \hline \\ & \approx 12BTSNH = 12BT^2NH \\ \end{array}\]

Note [causal masking]: 대부분의 최근 transformer는 완전 양방향 어텐션 대신 인과 마스크(causal mask)를 사용합니다. 이 경우 내적 연산의 유용한 FLOPs는 1/2로 줄어듭니다. 실제로 이 감소를 달성하려면 단순한 einsum이 아닌 attention kernel을 사용해야 합니다.

Other Operations

Transformer에는 몇 가지 다른 연산도 발생합니다. Layernorm은 비교적 저렴하므로 1차 비용 추정에서는 무시할 수 있습니다. 또한 마지막에 거대한(레이어별은 아니지만) unembedding 행렬 곱셈도 있습니다.

\[\begin{array}{ccc} \textsf{operation} & \textsf{train FLOPs} & \textsf{params} \\ \hline \\ \textrm{layernorm}_D \;\; A[B,T,\red{D}] & \gray{O\left(BTD\right)} & \gray{D} \\[10pt] A[B,T,\red{D}] \cdot W_{unembed}[\red{D}, V] & 6BTDV & DV \\ \end{array}\]

General rule of thumb for Transformer FLOPs

짧은 컨텍스트 훈련에 대해 내적 어텐션 비용을 무시한다면, 모든 레이어에 걸친 총 FLOPs는 다음과 같습니다.

\[\begin{align*} (18BTDF + 12BTD(N+K)H)L = 6 *BT * (3DF + 2D(N+K)H)L \\ = 6 * \textrm{num tokens} * \textrm{parameter count} \end{align*}\]

이는 어텐션 FLOPs를 무시하고 밀집(dense) Transformer FLOP 수를 추정하는 유명한 경험 법칙으로 이어집니다. (Unembedding은 $6BSDV$ FLOPs와 $DV$ 파라미터를 가진 또 다른 간단한 matmul이며, 동일한 경험 법칙을 따릅니다.)

Fractional cost of attention with context length

위에서 내적 어텐션을 고려하고 $F=4D$, $D=NH$(전형적인 경우), 그리고$N=K$라고 가정한다면:

\[\small{\frac{\textrm{attention FLOPs}}{\textrm{matmul FLOPs}} = \frac{12BT^2NH}{18BTDF + 24BTDNH} = \frac{12BT^2D}{4*18 BTD^2 + 24 BTD^2} = \frac{12BT^2D}{96 BTD^2} = \frac{T}{8D}}\]

따라서 요점은 내적 어텐션 FLOPs는 T>8D일 때만 훈련 중에 지배적이 된다는 것입니다. D ~ 8k의 경우, 이는 ~64K 토큰이 됩니다. 이는 MLP 크기가 커질수록 어텐션 FLOPs가 덜 중요해진다는 것을 의미하므로 일리가 있습니다. 대규모 모델의 경우, 어텐션의 2차 비용은 실제로 긴 컨텍스트 훈련에 큰 장애물이 되지 않습니다. 하지만 더 작은 모델, 예를 들어 Gemma-27B의 경우 D=4608이므로 32k 시퀀스 길이 정도에서 어텐션이 지배적이 됩니다. Flash Attention은 긴 컨텍스트의 비용을 완화하는 데 도움이 되며, 이에 대해서는 Appendix A에서 간단히 논의합니다.

Miscellaneous Math

Sparsity and Mixture-of-Experts

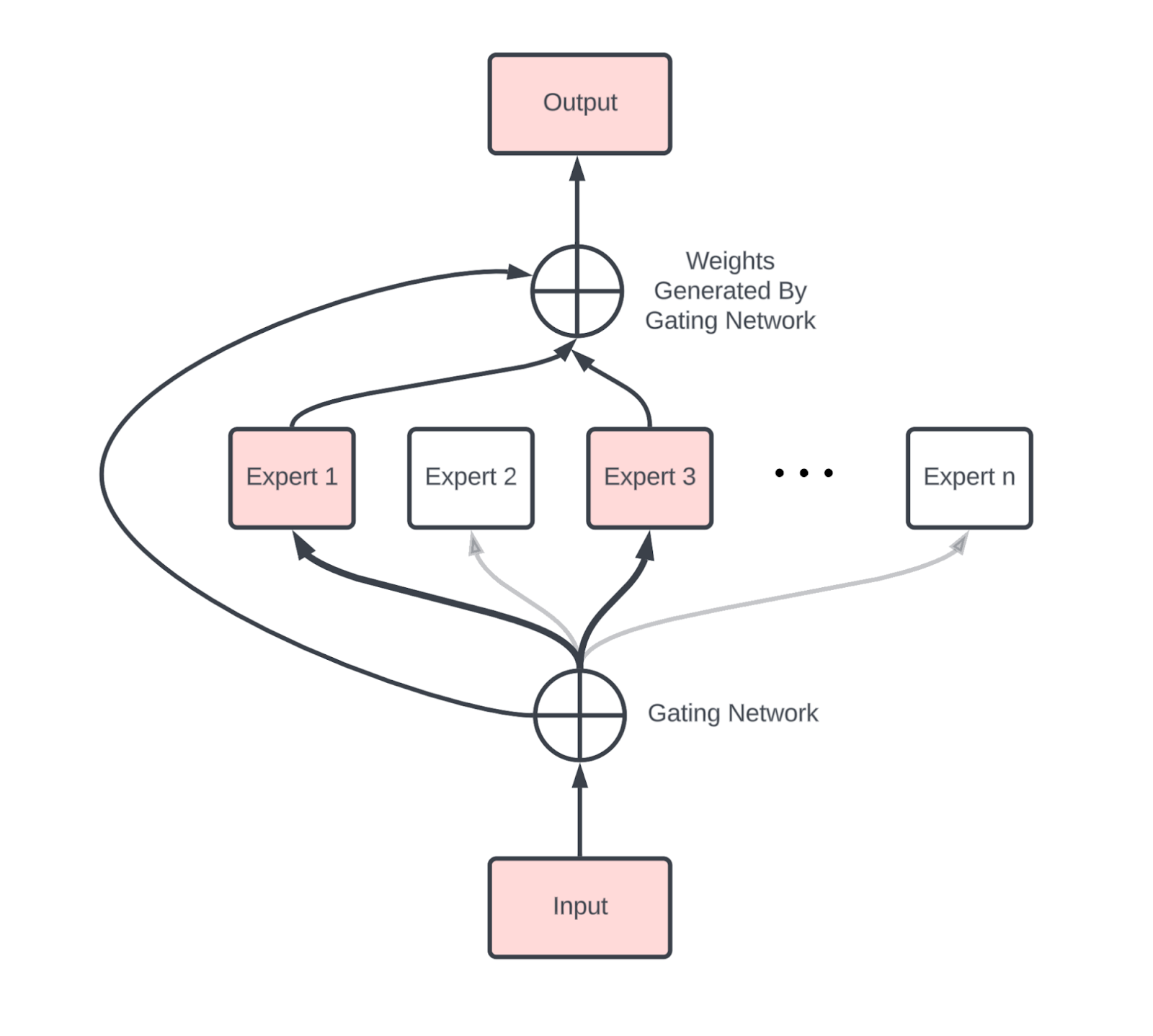
Mixture of Experts (MoE) 모델에 대해 간단히 논의하지 않고 넘어갈 수 없습니다. MoE는 표준 Transformer의 단일 밀집 MLP 블록을 동적으로 라우팅할 수 있는 독립적인 MLP 세트로 대체합니다. 1차 근사로, MoE는 단지 레이어당 하나가 아닌 E개의 MLP 블록을 가진 일반 밀집 모델입니다. 각 토큰은 $k$개의 전문가를 활성화하며, 일반적으로 $k \ll E$입니다. 비율 $E / k$를 희소성(sparsity)이라고 하며 보통 8에서 64 사이입니다 (예: DeekSeek v3는 사실상 $k=8$, $E=256$입니다). 이는 파라미터 수를 $O(E)$만큼 증가시키는 반면, 밀집 버전에 비해 토큰당 활성화된 파라미터 총 수에 $k$를 곱합니다.

**Figure:** $n$개의 전문가가 있는 예제 MoE 레이어. 게이팅 전문가는 각 토큰을 그 중 $k$개로 라우팅하고, 그 $k$개 MLP의 출력이 합산됩니다. 우리의 파라미터 수는 각 전문가 크기의 $n$배이지만, 각 토큰에 대해 $k$개만 사용됩니다. 출처.

밀집 모델과 비교할 때, MoE는 새로운 통신, 주로 두 개의 AllToAll(MoE 블록 전 하나, 후 하나)을 도입하여 토큰을 올바른 전문가에게 라우팅하고 다시 홈 디바이스로 가져옵니다.엄밀히 말하면, 이는 전문가와 동일한 축을 따라 데이터 또는 시퀀스가 샤딩된 경우에만 발생합니다. 그러나 이전 섹션에서 보았듯이, 각 AllToAll의 비용은 (양방향 링의 경우) 단일 축을 따른 유사한 AllGather의 1/4에 불과합니다.

Gradient checkpointing

알고리즘으로서의 역전파는 메모리와 연산을 교환합니다. 역방향 패스가 $O(n_\text{layers}^2)$FLOPs를 요구하는 대신, $O(n_\text{layers})$ 메모리를 요구하며, 순방향 패스 중에 생성된 모든 중간 활성화를 저장합니다. 이것이 2차 연산보다 낫긴 하지만, 메모리 측면에서는 엄청나게 비쌉니다.$B * T=4M$(배치당 4M 총 토큰), L=64, D=8192인 모델이 불필요한 역방향 패스 연산을 모두 피하려면 bfloat16에서 대략$2 * 20 * B * T * D * L = 84TB$의 활성화를 저장해야 합니다. 20은 위 Transformer 다이어그램의 모든 중간 노드를 (대략) 계산한 것입니다. 예를 들어

\[f(x) = \exp(g(x))\] \[\frac{df}{dx} = \exp(g(x)) \cdot \frac{dg}{dx}\]

이므로 재계산을 피하려면 순방향 패스에서 $g(x)$와 $\exp(g(x))$를 저장해야 합니다. 이렇게 많은 메모리를 저장하는 것을 피하기 위해, 중간 활성화의 일부만 저장하도록 선택할 수 있습니다. 다음은 우리가 사용하는 몇 가지 전략입니다.

Block remat: 각 레이어의 입력만 저장합니다. 이것은 우리가 사용하는 가장 공격적인 방법이며 레이어당 1개의 체크포인트만 저장하므로, 위 예제에서 4.2TB만 저장하게 됩니다. 이는 역방향 패스에서 사실상 모든 순방향 패스 FLOPs를 반복하게 하므로, FLOPs를 $6ND$에서 대략 $8ND$로 증가시킵니다.
Big matmuls only: 또 다른 간단한 정책은 큰 matmul의 출력만 저장하는 것입니다. 이를 통해 역방향 패스 중에 큰 matmul을 재계산하는 것을 피할 수 있지만, 여전히 다른 활성화 함수와 어텐션의 일부를 재계산하게 만듭니다. 이는 레이어당 20개를 7개 정도로 줄입니다.

이것이 전부는 아닙니다. JAX를 사용할 때, 이들은 일반적으로 jax.remat/jax.checkpoint에 의해 제어됩니다 (여기에서 더 읽어보세요).

Key-Value (KV) caching

섹션 7에서 보겠지만, LLM 추론에는 프리필(prefill)과 생성(generation)이라는 두 가지 핵심 부분이 있습니다.

Prefill은 긴 프롬프트를 처리하고 생성에 사용하기 위해 어텐션 활성화를 Key-Value Cache (KV Cache)에 저장합니다. 구체적으로 어텐션 블록의 키-값 projection입니다.
Generation은 여러 KV 캐시를 함께 배치하고 각각에서 토큰을 샘플링합니다.

그러면 각 KV 캐시는 사실상 $[2, S, L, K, H]$ 크기의 배열이 되며, 여기서 2는 키와 값을 설명합니다. 이것은 꽤 큽니다! int8에서 Key-Value 캐시의 총 크기는 $2SLKH$입니다. 8k 컨텍스트 길이, 64 레이어, $KH = NH = D = 8192$인 중간 크기 모델의 경우, 이는 $2 \cdot 8192 \cdot 64 \cdot 8192 = 8\text{GiB}$입니다. 왜 우리가 $K \ll N$인 GMQA를 사용하고 싶어하는지 알 수 있습니다.

What Should You Take Away from this Section?

Transformer의 전체 파라미터와 FLOPs는 계산하기 꽤 쉬우며, MHA (배치 크기 B, 어휘 크기 V, 길이 T의 시퀀스, D=d_model, F=d_ff)를 가정할 때 다음과 같이 요약됩니다:

Component	Params per layer	Training FLOPs per layer
MLP	3DF	18BTDF
Attention	4DNH	24BTDNH + 12BT²NH
Other	D	BTD
Vocab	DV (total, not per-layer)	12BTDV

MLP 블록의 파라미터 수는 전체 파라미터 수를 지배하며, 시퀀스 길이 $T < 8D$인 한 MLP 블록이 FLOPs 예산도 지배합니다.
훈련 중 총 FLOPs 예산은 합리적인 컨텍스트 길이에 대해 $6 \cdot \text{num_params} \cdot \text{num_tokens}$로 잘 근사됩니다.
추론 중, KV 캐시는 캐시당 대략 $2 \cdot S \cdot L \cdot N \cdot H$이지만, 아키텍처 수정으로 종종 이를 줄일 수 있습니다.

A Few Problems to Work

Question 1: $D=4096$, $F=4 \cdot D$, $V=32,000$, $L=64$인 모델은 얼마나 많은 파라미터를 가질까요? 이 중 어텐션 파라미터의 비율은 얼마인가요? 토큰당 KV 캐시의 크기는 얼마인가요? $N\cdot H=D$와 int8 KV를 사용하는 멀티 헤드 어텐션을 가정할 수 있습니다.

답을 보려면 여기를 클릭하세요.

총 파라미터는 대략 $L \cdot (3DF + 4DNH + D) + 2DV$입니다. 주어진 숫자에 대해 이는 $64 \cdot (3 \cdot 4e3 \cdot 16e3 + 4 \cdot 4e3 \cdot 4e3 + 4e3) + 2 \cdot 4e3 \cdot 32e3 = 16e9$, 즉 16B 파라미터입니다.
어텐션 파라미터 대 전체 파라미터의 비율은 일반적으로 $4DNH / (4DNH + 3DF) = 4D^2 / (4D^2 + 12D^2) = 1/4$입니다. 이는 파라미터의 대략 1/4이 어텐션에 사용됨을 의미합니다.
토큰당, KV 캐시는 int8에서 $2 \cdot L \cdot N \cdot H = 2 \cdot 64 \cdot 4096$이며, 이는 512kB / token입니다.

Question 2: {‘X': 4, ‘Y': 8, ‘Z': 4}에서 A[B_X, D_Y] *_D W[D_Y, F]를 수행하는 데 필요한 총 FLOPs는 얼마인가요? 각 TPU에서 수행되는 FLOPs는 얼마인가요?

답을 보려면 여기를 클릭하세요.

연산의 총 “이론적” FLOPs는 $2 \cdot B \cdot D \cdot F$입니다. 하지만 계산이 Z 차원에 대해 샤딩되지 않았기 때문에, 실제로 Z배 추가 FLOPs를 수행하고 있으므로 총 FLOPs는 $2 \cdot B \cdot D \cdot F \cdot Z$입니다. 계산이 다른 차원에 걸쳐 샤딩되므로, 디바이스당 총량은 대략 $2 \cdot B \cdot D \cdot F / (X \cdot Y)$입니다.

Question 3: $A[I,J,K,L] * B[I,J,M,N,O] \rightarrow C[K,L,M,N,O]$를 수행하는 데 얼마나 많은 FLOPs가 포함되나요?

답을 보려면 여기를 클릭하세요.

위 규칙에 따르면, I와 J는 축약 차원이고 K, L, M, N, O는 비축약 차원입니다. “배치 차원”이 없으므로, 이는 단지 $2 \cdot I \cdot J \cdot K \cdot L \cdot M \cdot N \cdot O$, 즉 모든 축의 곱입니다. 공유된 축이 있었다면 한 번만 계산되었을 것입니다.

Question 4: Self-attention(Q/K/V/O projections 무시)의 arithmetic intensity는 얼마인가요? Q와 KV 길이 T와 S의 함수로 답을 제시하세요. 어떤 컨텍스트 길이에서 어텐션이 FLOPs-bound가 되나요? TPU의 HBM 대역폭이 주어졌을 때, 컨텍스트 길이가 증가함에 따라 FFW 블록에 대한 어텐션의 유효 상대 비용을 플롯하세요.

답을 보려면 여기를 클릭하세요.

Self-attention은 $Q$, $K$, $V$활성화를 로드한 다음,$\text{softmax}(Q \cdot K) \cdot V$를 계산하고, 결과를 HBM에 다시 써야 합니다. Flash Attention으로 수행되므로 이 수학에는 몇 가지 주의 사항이 있지만, 기본적으로 bf16 self-attention은 다음을 수행합니다.

\[\text{Q[B,T,N,H]} \rightarrow_\text{reshape} \text{Q[B, T, K, G, H]} \cdot \text{K[B, S, K, H]} \rightarrow \text{O[B, T, S, K, G]}\] \[U=\text{softmax}_S(\text{O[B, T, S, K, G]})\] \[\text{U[B, T, S, K, G]} \cdot \text{V[B, S, K, H]} \rightarrow \text{X[B, T, K, G, H]}\]

따라서 총 바이트는 $2 * \text{sizeof}(Q) + 2 * \text{sizeof(K or V)} = 4BTNH + 4BSKH = 4BHK * (TG + S)$이고, 총 FLOPs는 $4BTSNH + O(BTSN)$이며 arithmetic intensity는 $4BTSKGH / (4BHK * (TG + S))$입니다.

따라서 기본적으로, 프리필 중에는 $S=T$이므로 arithmetic intensity는 $4BT^2KGH / 4BHKT \cdot (G+1) = TG/(G + 1) = O(T)$입니다. 생성 중에는 $T=1$이므로 $4BSKGH / (4BHK \cdot (G + S)) = SG / (G + S) \rightarrow G$이며 $S$가 매우 크다고 가정합니다. 질문을 어떻게 해석하느냐에 따라, 시퀀스 샤딩이 없다고 가정할 때 S=240에서 프리필 또는 훈련 중 self-attention은 compute bound입니다. 생성 중에는 $G$가 작기 때문에 결코 compute bound가 아닙니다. 그럼에도 불구하고, $G$를 늘리면 compute bound에 더 가까워지는 것을 볼 수 있습니다.

Question 5: 어떤 시퀀스 길이에서 self-attention FLOPs가 QKVO projection FLOPs와 같아지나요?

답을 보려면 여기를 클릭하세요.

이는 순전히 $24BTDNH == 12BT^2NH$일 때의 문제입니다. 단순화하면 $2D = T$가 되므로, 예를 들어 $D=4096$의 경우 $8192$입니다. 이는 대부분의 합리적인 컨텍스트 길이에 대해 matmul FLOPs가 더 크다는 것을 알려줍니다.

Question 6: 순방향 패스 중에 Transformer 레이어의 7개 주요 matmul(Q, K, V, O + 세 개의 FFW 행렬) 각각의 출력만 저장한다고 가정해 봅시다. 역방향 패스 중에 “재생성(rematerialize)”하기 위해 얼마나 많은 추가 FLOPs가 필요한가요?

답을 보려면 여기를 클릭하세요.

7개의 matmul 출력(Q, K, V, O, W₁, W₂, W₃)만 저장한다는 것은 역방향 패스에서 두 개의 어텐션 matmul을 재계산해야 함을 의미합니다.

\[QK^{\top} \quad\text{and}\quad \operatorname{softmax}(QK^{\top})V.\]

각각은 $B$ 시퀀스와 $N$ 헤드에 걸쳐 배치된 $T \times T$ matmul이므로, 추가 FLOPs는 다음과 같습니다.

\[4 \; B \, T^{2} \, N \, H.\]

다른 모든 재계산된 연산은 $O(BTD)$에 불과합니다.

Question 7: DeepSeek v3는 14.8T 토큰에 대해 2.79M H800 시간 동안 훈련되었다고 합니다 (출처). 37B 활성화 파라미터를 가지고 있다고 할 때, 대략 어느 정도의 하드웨어 활용률(utilization)을 달성했나요? 힌트: 구조적 희소성 없이 FP8 FLOPs를 사용했다는 점에 유의하세요.

답을 보려면 여기를 클릭하세요.

여기 사양 시트에서, 희소성 포함 FP8 성능이 3,026 TFLOPs/s임을 알 수 있으며, 희소성 없이는 일반적으로 이의 절반(1.513e15 FLOPs/s)입니다. 2.79M H800 시간은 2.79e6 * 1.513e15 * 60 * 60 = 1.52e25 총 FLOPs를 의미합니다. 37B 활성화 파라미터 수를 고려할 때, 이 훈련 실행은 약 6 * 37e9 * 14.8e12 = 3.3e24 FLOPs를 사용했을 것입니다. 이는 FLOPs 활용률이 약 3.3e24 / 1.52e25 = 21.7%임을 의미합니다.

Question 8: Mixture of Experts (MoE) 모델은 표준 밀집 MLP 블록의 $E$개 사본을 가지고 있으며, 각 토큰은 이 중 $k$개의 전문가를 활성화합니다. TPU v5e에서 int8 가중치를 가진 MoE가 compute-bound가 되기 위해 필요한 토큰 단위 배치 크기는 얼마인가요? 256개의 (라우팅된) 전문가와 $k=8$을 가진 DeepSeek의 경우, 이 숫자는 얼마인가요?

답을 보려면 여기를 클릭하세요.

각 전문가의 $E$개 사본을 가지고 있으므로, int8에서 $E \cdot D \cdot F$ 바이트를 로드해야 합니다. 각 토큰이 $k$개의 전문가를 활성화하므로, $2\cdot k \cdot B \cdot D \cdot F$ FLOPs를 가집니다. bfloat16 FLOPs로 compute-bound가 되려면 arithmetic intensity가 240을 넘어야 하며, 이는 $(2\cdot k \cdot BDF) / EDF > 240$ 또는 $k \cdot B / E > 120$일 때 발생합니다.

따라서 compute bound가 되려면 $B > 120 \cdot E / k$여야 합니다. DeepSeek의 경우, 이는 $B > 120 \cdot 256 / 8 = 3840$을 제공합니다. 이는 생성 시에 놀라울 정도로 큰 배치 크기입니다.

파트 4는 여기까지입니다! 파트 5(트랜스포머 훈련 확장에 관한 내용)를 보려면, 여기를 클릭하세요!

Appendix

Appendix A: How does Flash Attention work?

트랜스포머를 매우 긴 컨텍스트로 확장하는 것에 대한 전통적인 반대 의견은 어텐션 FLOPs와 메모리 사용량이 컨텍스트 길이에 따라 2차적으로 증가한다는 것입니다. 어텐션 QK 곱이 $[B, S, T, N]$ 형태를 가지며 여기서 B는 배치 크기, S와 T는 Q와 K 시퀀스 차원, N은 헤드 수라는 것은 사실이지만, 이 주장에는 몇 가지 심각한 주의 사항이 따릅니다:

섹션 4에서 언급했듯이, 이것이 2차적이라 할지라도 어텐션 FLOPs는 $S > 8 \cdot D$일 때만 지배적이었으며, 특히 훈련 중에 단일 어텐션 행렬의 메모리는 메모리에 있는 모든 가중치 및 활성화 체크포인트에 비해 작습니다(특히 샤딩될 때).
어텐션을 계산하기 위해 전체 어텐션 행렬을 구체화(materialize)할 필요가 없습니다! 로컬 합계와 최대값을 계산하고 배열의 작은 청크 이상을 구체화하는 것을 피할 수 있습니다. 총 FLOPs는 여전히 2차적이지만, 메모리 압박을 크게 줄입니다.

이 두 번째 관찰은 Rabe et al. 2021에서 처음 이루어졌고 나중에 Flash Attention 논문 (Dao et al. 2022)에서 이루어졌습니다. 기본 아이디어는 K/V의 청크로 어텐션을 계산하는 것인데, 여기서 로컬 softmax와 일부 보조 통계를 계산한 다음, 이를 다음 청크로 전달하여 로컬 청크와 결합합니다. 구체적으로 우리는 다음을 계산합니다.

M: 시퀀스 차원에 대한 $q \cdot k$의 실행 최대값(running max)
O: 시퀀스 차원에 대한 실행 전체 어텐션 softmax
L: 실행 분모(running denominator) $\sum_i (q \cdot k_i - \text{running max})$

이것들로 우리는 일정한 양의 메모리만으로 새로운 최대값, 새로운 실행 합계, 새로운 출력을 계산할 수 있습니다. 이것이 어떻게 작동하는지 대략적으로 설명하자면, 어텐션은 대략 다음과 같은 연산입니다:

\[\text{Attn}(Q, K, V) = \sum_i \frac{\exp(Q \cdot K_i - \max_j Q \cdot K_j) V_i}{\sum_l \exp(Q \cdot K_l - \max_j Q \cdot K_j)}\]

최대값은 수치적 안정성을 위해 빼지며, $\sum_i \exp(a_i + b) = \exp(b) \sum \exp(a)$이므로 결과에 영향을 주지 않고 더할 수 있습니다. 위의 분모만 보면, 두 개의 연속적인 키 벡터 청크 $K^1$과 $K^2$가 있다고 상상하고 각각에 대해 로컬 softmax 합 $L^1$과 $L^2$를 계산한다고 합시다.

\[L^1 = \sum_i \exp(Q \cdot K_i^1 - \max_j Q \cdot K_j^1)\] \[L^2 = \sum_i \exp(Q \cdot K_i^2 - \max_j Q \cdot K_j^2)\]

그러면 다음을 사용하여 이 두 청크를 합친 전체 softmax 합으로 결합할 수 있습니다.

\[L^\text{combined} = \exp(M^1 - \max(M^1, M^2)) \cdot L^1 + \exp(M^2 - \max(M^1, M^2)) \cdot L^2\]

여기서

\[M^1 = \max_j Q \cdot K_j^1 \text{ and } M^2 = \max_j Q \cdot K_j^2\]

이는 전체 softmax에 대해서도 수행할 수 있어, 임의로 큰 softmax 합을 누적하는 방법을 제공합니다. 다음은 Flash Attention 논문의 전체 알고리즘입니다.

하드웨어 관점에서 볼 때, 이를 통해 Q 청크를 VMEM(위 알고리즘에서는 온칩 SRAM이라고 함)에 맞출 수 있으므로 각 반복마다 KV 청크만 로드하면 되어 arithmetic intensity를 줄일 수 있습니다. 또한 실행 통계(running statistics)를 VMEM에 유지할 수 있습니다.

강조할 만한 마지막 미묘한 점은 훈련을 위한 Flash VJP (역방향 모드 미분) 계산을 실용적으로 만드는 데 사용되는 어텐션 softmax 속성입니다. 중간 softmax 배열을 다음과 같이 정의하면:

\[S_{ij} = \frac{e^{\tau q_i \cdot k_j}}{\sum_k e^{\tau q_i \cdot k_j}}\]

어텐션에서 역방향 모드 dO 및 V 배열로부터 dS를 얻습니다:

\[dS_{ij} = dO_{id} \cdot_d V_{jd} = \sum_d dO_{id} V_{jd}\]

이 그래디언트를 Q와 K로 역전파하는 동안

\[d(q_i \cdot k_j) = (dS_{ij} - S_{ij} \cdot_j dS_{ij}) S_{ij}\]

우리는 큰 키 길이 차원을 따른 축약을 특징 깊이 차원을 따른 로컬 축약으로 교환할 수 있게 하는 항등식을 활용합니다.

\[\begin{align*} S_{ij} \cdot_j dS_{ij} &= \sum_j \frac{e^{\tau q_i \cdot k_j}}{\sum_k e^{\tau q_i \cdot k_k}} \sum_d dO_{id} V_{jd} \\ &= \sum_d dO_{id} \sum_j \frac{e^{\tau q_i \cdot k_j}}{\sum_k e^{\tau q_i \cdot k_k}} V_{jd} \\ &= \sum_d dO_{id} O_{id} \\ &= dO_{id} \cdot_d O_{id} \end{align*}\]

이 교체는 VJP에 대해 시퀀스 블록 로컬 계산을 구현할 수 있게 하는 데 중요하며, 링 어텐션과 같은 더 기발한 샤딩 계획을 가능하게 합니다.

Miscellaneous

^*Work done at Google DeepMind, now at MatX.

Citation

For attribution in academic contexts, please cite this work as:

    Austin et al., "How to Scale Your Model", Google DeepMind, online, 2025.

or as a BibTeX entry:

    @article{scaling-book,
      title = {How to Scale Your Model},
      author = {Austin, Jacob and Douglas, Sholto and Frostig, Roy and Levskaya, Anselm and Chen, Charlie and Vikram, Sharad
      and Lebron, Federico and Choy, Peter and Ramasesh, Vinay and Webson, Albert and Pope, Reiner},
      publisher = {Google DeepMind},
      howpublished = {Online},
      note = {Retrieved from https://jax-ml.github.io/scaling-book/},
      year = {2025}
    }